题目内容
设函数f(x)=x3-x2-3,g(x)=
+xlnx,其中a∈R.
(1)若存在x1,x2∈[0,2],使得f(x1)-f(x2)≥M,求整数M的最大值;
(2)若对任意的s,t∈[
,2],都有f(t)≤g(s),求a的取值范围.
| a |
| x |
(1)若存在x1,x2∈[0,2],使得f(x1)-f(x2)≥M,求整数M的最大值;
(2)若对任意的s,t∈[
| 1 |
| 2 |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的概念及应用
分析:(1)f′(x)=3x(x-
),x∈[0,2],令f'(x)=0,得x1=0,x2=
,列表讨论能求出整数M的最大值.
(2)由(1)知,在[
,2]上,[f(x)]max=f(2)=1,要满足对任意的s,t∈[
,2],都有f(t)≤g(s),只需g(x)≥1在[
,2]上恒成立,由此能求出a的取值范围.
| 2 |
| 3 |
| 2 |
| 3 |
(2)由(1)知,在[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:(1)f′(x)=3x(x-
),x∈[0,2],令f'(x)=0得x1=0,x2=
,…(2分)
当x变化时,f'(x)和f(x)的变化情况如下:
可得,[f(x)]max=1,[f(x)]min=f(
)=-
.…(5分)
要使存在x1,x2∈[0,2],使得f(x1)-f(x2)≥M,只需M≤[f(x)]max-[f(x)]min=
,故整数M的最大值为4.…(7分)
(2)由(1)知,在[
,2]上,[f(x)]max=f(2)=1,要满足对任意的s,t∈[
,2],都有f(t)≤g(s),只需g(x)≥1在[
,2]上恒成立,…(9分)
即
+xlnx≥1在[
,2]上恒成立,分离参数可得:a≥x-x2lnx,
令h(x)=x-x2lnx,h'(x)=1-x-2xlnx,可知,当x∈[
,1),h′(x)>0,h(x)单调递增,当x∈(1,2],h'(x)<0,h(x)单调递减,…(12分)
所以h(x)在x=1处取得最大值h(1)=1,
所以a的取值范围是a≥1.…(13分)
| 2 |
| 3 |
| 2 |
| 3 |
当x变化时,f'(x)和f(x)的变化情况如下:
| x | 0 | (0,
|
| (
| 2 | ||||||
| f'(x) | - | 0 | + | ||||||||
| f(x) | -3 | 单调递减 | 极小值 | 单调递增 | 1 |
| 2 |
| 3 |
| 85 |
| 27 |
要使存在x1,x2∈[0,2],使得f(x1)-f(x2)≥M,只需M≤[f(x)]max-[f(x)]min=
| 112 |
| 27 |
(2)由(1)知,在[
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即
| a |
| x |
| 1 |
| 2 |
令h(x)=x-x2lnx,h'(x)=1-x-2xlnx,可知,当x∈[
| 1 |
| 2 |
所以h(x)在x=1处取得最大值h(1)=1,
所以a的取值范围是a≥1.…(13分)
点评:本题主要考查最值的概念、利用导数研究函数的单调性等基础知识,同时考查推理论证能力,分类讨论等综合解题能力.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
在如图程序中,要使输入的X和输出的Y值相等,则满足条件的X的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
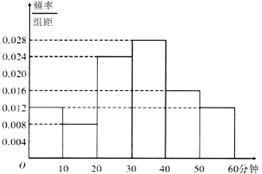 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.