题目内容
直线y=kx+3与圆(x-3)2+(y-2)2=4相交于M,N两点,若|MN|≥2
,则k的取值范围是 .
| 3 |
考点:直线与圆的位置关系
专题:直线与圆
分析:由圆的方程找出圆心坐标与半径r,利用点到直线的距离公式表示出圆心到直线的距离d,利用垂径定理及勾股定理表示出弦长|MN|,列出关于k的不等式,求出不等式的解集即可得到k的范围.
解答:
解:由圆的方程得:圆心(3,2),半径r=2,
∵圆心到直线y=kx+3的距离d=
,|MN|≥2
,
∴2
=2
≥2
,
变形得:4-
≥3,即8k2+6k≤0,
解得:-
≤k≤0,
则k的取值范围是[-
,0].
故答案为:[-
,0]
∵圆心到直线y=kx+3的距离d=
| |3k-2+3| | ||
|
| 3 |
∴2
| r2-d2 |
4-
|
| 3 |
变形得:4-
| (3k+1)2 |
| k2+1 |
解得:-
| 3 |
| 4 |
则k的取值范围是[-
| 3 |
| 4 |
故答案为:[-
| 3 |
| 4 |
点评:此题考查了直线与圆相交的性质,涉及的知识有:圆的标准方程,点到直线的距离公式,垂径定理,勾股定理,熟练掌握公式及定理是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
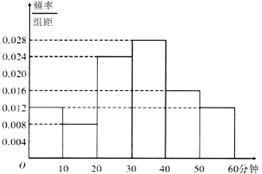 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”. 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).