题目内容
已知等比数列{an}的各项均为正数,且a1+4a2=1,a32=16a2a6.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,求数列{
}的前n项和Tn.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=log2an,求数列{
| 1 |
| bnbn+1 |
考点:数列的求和,等比数列的通项公式
专题:综合题,等差数列与等比数列
分析:(Ⅰ)设数列{an}的公比为q,通过解方程组可求得a1与q,从而可求数列{an}的通项公式;
(Ⅱ)利用裂项法可求得数列{
}的前n项和Tn.
(Ⅱ)利用裂项法可求得数列{
| 1 |
| bnbn+1 |
解答:
解:(Ⅰ)设数列{an}的公比为q,由a32=16a2a6得a32=16a42所以q2=
.
由条件可知q>0,故q=
.
由a1+4a2=1得a1+4a1q=1,所以a1=
.
故数列{an}的通项为an=
;
(Ⅱ)bn=log2an=-(2n-1),
所以
=
(
-
),
所以Tn=
(1-
+
-
+…+
-
)=
(1-
)=
.
| 1 |
| 16 |
由条件可知q>0,故q=
| 1 |
| 4 |
由a1+4a2=1得a1+4a1q=1,所以a1=
| 1 |
| 2 |
故数列{an}的通项为an=
| 1 |
| 22n-1 |
(Ⅱ)bn=log2an=-(2n-1),
所以
| 1 |
| bnbn+1 |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
所以Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题主要考查了等比数列的性质及其应用,第二问难度有些大,利用裂项法进行求和,这是数列求和常用的方法,此题是一道中档题.

练习册系列答案
相关题目
若曲线f(x)=ax3+lnx存在垂直于y轴的切线,则实数a的取值范围( )
| A、(1,+∞) |
| B、(-∞,1) |
| C、(0,+∞) |
| D、(-∞,0) |
已知集合M={x|-2<x<2},N={x|x<1},则M∩N等于( )
| A、(-2,1) | B、(1,2) |
| C、∅ | D、(-∞,2) |
若集合A={x||x-3|<2},B={x|x≥3},那么A∩B=( )
| A、(1,3] |
| B、[3,5) |
| C、(3,+∞] |
| D、[3,5] |
在如图程序中,要使输入的X和输出的Y值相等,则满足条件的X的个数是( )


| A、1个 | B、2个 | C、3个 | D、4个 |
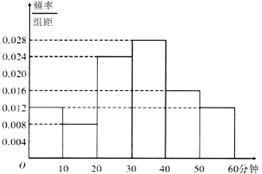 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.