题目内容
设函数f(x)=ax+
(a<0).
(Ⅰ)若函数f(x)在(1,+∞)上为减函数,求实数a的最大值;
(Ⅱ)若存在x1,x2∈[
,e2],使f(x1)≤f′(x2)-a成立,求实数a的取值范围.
| x |
| lnx |
(Ⅰ)若函数f(x)在(1,+∞)上为减函数,求实数a的最大值;
(Ⅱ)若存在x1,x2∈[
| e |
考点:利用导数研究函数的极值,利用导数研究函数的单调性
专题:导数的综合应用
分析:(Ⅰ)由已知得f(x)的定义域为(0,1)∪(1,+∞),f′(x)=a+
≤0在(1,+∞)上恒成立,由此利用导数性质能求出a的最大值.
(Ⅱ)命题“若存在x1,x2∈[
,e2],使f(x1)≤f′(x2)-a成立”,等价于“当x∈[
,e2]时,有f(x)min≤f′(x)max-a”,由此利用导数性质结合分类讨论思想能求出实数a的取值范围.
| lnx-1 |
| (lnx)2 |
(Ⅱ)命题“若存在x1,x2∈[
| e |
| e |
解答:
解:(Ⅰ)由已知得f(x)的定义域为(0,1)∪(1,+∞),
∵f(x)在(1,+∞)上为减函数,
∴f′(x)=a+
≤0在(1,+∞)上恒成立,
a≤
-
=(
-
)2-
,
令g(x)=(
-
)2-
,
故当
=
,即x=e2时,
g(x)的最小值为-
,∴a≤-
,
∴a的最大值为-
.
(Ⅱ)命题“若存在x1,x2∈[
,e2],使f(x1)≤f′(x2)-a成立”,
等价于“当x∈[
,e2]时,有f(x)min≤f′(x)max-a”,
由(Ⅰ)知,当x∈[
,e2]时,lnx∈[
,2],
∈[
,2],
f′(x)=a+
=-(
-
)2+
+a,
f′(x)max-a=
,
问题等价于:“当x∈[
,e2]时,有f(x)min≤
”,
①当a≤-
时,由(Ⅰ),f(x)在[
,e2]上为减函数,
则f(x)min=f(e2)=ae2+
≤
,
∴a≤
-
-
,
∴a≤
-
.
②当-
<a<0时,∵x∈[
,e2],∴lnx∈[
,2],
∵f′(x)=a+
,由复合函数的单调性知f′(x)在[
,e2]上为增函数,
∴存在唯一x0∈(
,e2),使f′(x0)=0且满足:
f(x)min=f(x0)=ax0+
,
要使f(x)min≤
,∴a≤
-
<
-
=-
,
与-
<a<0矛盾,
∴-
<a<0不合题意,
综上,实数a的取值范围为(-∞,
-
].
∵f(x)在(1,+∞)上为减函数,
∴f′(x)=a+
| lnx-1 |
| (lnx)2 |
a≤
| 1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
令g(x)=(
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
故当
| 1 |
| lnx |
| 1 |
| 2 |
g(x)的最小值为-
| 1 |
| 4 |
| 1 |
| 4 |
∴a的最大值为-
| 1 |
| 4 |
(Ⅱ)命题“若存在x1,x2∈[
| e |
等价于“当x∈[
| e |
由(Ⅰ)知,当x∈[
| e |
| 1 |
| 2 |
| 1 |
| lnx |
| 1 |
| 2 |
f′(x)=a+
| lnx-1 |
| (lnx)2 |
| 1 |
| lnx |
| 1 |
| 2 |
| 1 |
| 4 |
f′(x)max-a=
| 1 |
| 4 |
问题等价于:“当x∈[
| e |
| 1 |
| 4 |
①当a≤-
| 1 |
| 4 |
| e |
则f(x)min=f(e2)=ae2+
| e2 |
| 2 |
| 1 |
| 4 |
∴a≤
| 1 |
| 4e2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴a≤
| 1 |
| 4e2 |
| 1 |
| 2 |
②当-
| 1 |
| 4 |
| e |
| 1 |
| 2 |
∵f′(x)=a+
| lnx-1 |
| (lnx)2 |
| e |
∴存在唯一x0∈(
| e |
f(x)min=f(x0)=ax0+
| x0 |
| lnx0 |
要使f(x)min≤
| 1 |
| 4 |
| 1 |
| 4x0 |
| 1 |
| lnx0 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
与-
| 1 |
| 4 |
∴-
| 1 |
| 4 |
综上,实数a的取值范围为(-∞,
| 1 |
| 4e2 |
| 1 |
| 2 |
点评:本题主要考查函数、导数等基本知识.考查运算求解能力及化归思想、函数方程思想、分类讨论思想的合理运用,注意导数性质的合理运用.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
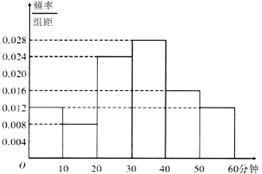 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.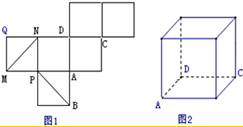 图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).