题目内容
已知数列{an}是等差数列,且a2=5,a4=9,数列{bn}正项的等比数列,Sn是其前n项和,且S2=
,S4=
,数列{cn},通项cn=an•bn,则求{cn}的前n项和Tn.
| 3 |
| 2 |
| 15 |
| 8 |
考点:数列的求和
专题:等差数列与等比数列
分析:利用待定系数法,设首项和公差及公比,由已知列方程组,可得数列{an}和{bn}的通项公式,进而利用错位相减的方法求得Tn.(一个等差数列和一个等比数列对应项之积组成的数列,可用错位相减法求和)
解答:
解:设等差数列{an}的公差为d,正项等比数列{bn}的公比为q(q>0),
由a2=5,a4=9,可得d=2,
故an=2n+1,
由S2=
,S4=
,可得S4-S2=
,
故
=q2=
,
故q=
,b1=1,
故bn=(
)n-1,
故cn=an•bn=(2n+1)(
)n-1,
∴Tn=3×1+5×
+7×(
)2+9×(
)3+…+(2n-1)(
)n-2+(2n+1)(
)n-1,…①
Tn=3×
+5×(
)2+7×(
)3+…+(2n-3)(
)n-2+(2n-1)(
)n-1+(2n+1)(
)n,…②
①-②得:
Tn=3+2×
+2×(
)2+2×(
)3+…+2×(
)n-1-(2n+1)(
)n
=1+4[1-(
)n]-(2n+1)(
)n=5-(2n+5)(
)n
故Tn=10-(4n+10)(
)n
由a2=5,a4=9,可得d=2,
故an=2n+1,
由S2=
| 3 |
| 2 |
| 15 |
| 8 |
| 3 |
| 8 |
故
| S4-S2 |
| S2 |
| 1 |
| 4 |
故q=
| 1 |
| 2 |
故bn=(
| 1 |
| 2 |
故cn=an•bn=(2n+1)(
| 1 |
| 2 |
∴Tn=3×1+5×
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
①-②得:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=1+4[1-(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
故Tn=10-(4n+10)(
| 1 |
| 2 |
点评:本题是数列求通项和前n项和的题型,高考常见,其中:
(1)可利用利用待定系数法求解,这是解数列题的一般方法,要熟练掌握.
(2)对于一个等差数列和一个等比数列对应项之积组成的数列,可用错位相减法求和,这也是教材推导等比数列前n项和公式时的方法.另外数列求和的方法还有倒序相加,裂项相消,分组求和等方法,要熟练掌握.都是高考中常考的知识点.
(1)可利用利用待定系数法求解,这是解数列题的一般方法,要熟练掌握.
(2)对于一个等差数列和一个等比数列对应项之积组成的数列,可用错位相减法求和,这也是教材推导等比数列前n项和公式时的方法.另外数列求和的方法还有倒序相加,裂项相消,分组求和等方法,要熟练掌握.都是高考中常考的知识点.

练习册系列答案
相关题目
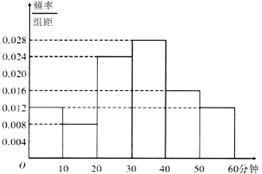 央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.
央视传媒为了解央视举办的“中国汉字听写大会”节目的收视情况,随机抽取了某市50名电视观众进行调查,下面是根据调查结果绘制的观众日均收看该节目时间的频率分布直方图.将收看“中国汉字听写大会”日均时间不低于30分钟的观众称为“汉语关注者”.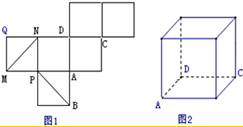 图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题
图1是一个正方体的表面展开图,MN和PB是两条面对角线,请在图2的正方体中将MN和PB画出来,并就这个正方体解决下列问题 如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).
如图1,平面四边形ABCD中,AB=AD,BC=CD,对角线AC与BD交于点O,AO=4,CO=2.将△BCD沿BD向上折起得四面体ABC′D(如图2).