题目内容
直线l过点A（2，π）且与极轴垂直，求l的极坐标方程．
考点：简单曲线的极坐标方程
专题：坐标系和参数方程
分析：设P（ρ，θ）为直线l上的任意一点，则2=ρcos（π-θ），即可得出．
解答：
解：如图所示，
设P（ρ，θ）为直线l上的任意一点，
则2=ρcos（π-θ），
化为2+ρcosθ=0．
∴l的极坐标方程为2+ρcosθ=0．
设P（ρ，θ）为直线l上的任意一点，
则2=ρcos（π-θ），
化为2+ρcosθ=0．
∴l的极坐标方程为2+ρcosθ=0．
点评：本题考查了直线的极坐标方程、直角三角形的边角关系，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
若x∈R，则“x＜1”是“|x|＜1”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知tanθ=2，则2sin2θ+sinθcosθ-cos2θ=（ ）
A、-
| ||
B、-
| ||
C、
| ||
D、
|
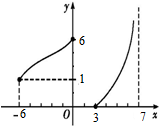函数y=f（x）的图象如图所示，则函数y=f（x）的定义域为