Question

7．在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，AC=2，二面角P-BC-A的大小为60°，三棱锥P-ABC的体积为$\frac{{4\sqrt{6}}}{3}$，则直线PB与平面PAC所成的角的正弦值为$\frac{\sqrt{3}}{3}$．

Answer 1

分析 由已知推导出∠PBA=60°，PA=2$\sqrt{3}$，BC=2$\sqrt{2}$，以C为原点，CA为x轴，CB为y轴，过C作平面ABC的垂线为z轴，建立空间直角坐标系，利用向量法能求出直线PB与平面PAC所成的角的正弦值．

解答 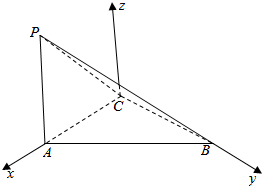解：∵在三棱锥P-ABC中，PA⊥底面ABC，AC⊥BC，AC=2，
∴∠PBA是二面角P-BC-A的平面角，
∵二面角P-BC-A的大小为60°，
∴∠PBA=60°，∴PB=4，PA=2$\sqrt{3}$，
∵三棱锥P-ABC的体积为$\frac{{4\sqrt{6}}}{3}$，
∴$\frac{1}{3}×2\sqrt{3}×\frac{1}{2}×2×BC=\frac{4\sqrt{6}}{3}$，解得BC=2$\sqrt{2}$，
以C为原点，CA为x轴，CB为y轴，过C作平面ABC的垂线为z轴，建立空间直角坐标系，
P（2，0，2$\sqrt{3}$），B（0，2$\sqrt{2}$，0），$\overrightarrow{PB}$=（-2，2$\sqrt{2}$，-2$\sqrt{3}$），
平面PAC的法向量$\overrightarrow{n}$=（0，1，0），
设直线PB与平面PAC所成的角为θ，
则sinθ=|cos＜$\overrightarrow{PB}$，$\overrightarrow{n}$＞|=|$\frac{\overrightarrow{PB}•\overrightarrow{n}}{|\overrightarrow{PB}|•|\overrightarrow{n}|}$|=|$\frac{2\sqrt{2}}{\sqrt{4+8+12}}$|=$\frac{\sqrt{3}}{3}$．
∴直线PB与平面PAC所成的角的正弦值为$\frac{\sqrt{3}}{3}$．
故答案为：$\frac{{\sqrt{3}}}{3}$．

点评 本题考查线面角的正弦值的求法，是中档题，解题时要认真审题，注意向量法的合理运用．