题目内容
已知F1、F2是椭圆的两个焦点,P为椭圆上一点,∠F1PF2=60°.
(1)求椭圆离心率的范围;
(2)求证:△F1PF2的面积只与椭圆的短轴长有关.
(1)解 法一 设椭圆方程为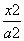 +
+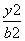 =1(a>b>0),
=1(a>b>0),
|PF1|=m,|PF2|=n,则m+n=2a.
在△PF1F2中,由余弦定理可知,
4c2=m2+n2-2mncos 60°=(m+n)2-3mn
=4a2-3mn≥4a2-3·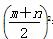 =4a2-3a2=a2(当且仅当m=n时取等号).∴
=4a2-3a2=a2(当且仅当m=n时取等号).∴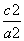 ≥
≥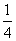 ,即e≥
,即e≥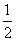 .
.
又0<e<1,∴e的取值范围是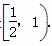 .
.
法二 如图所示,设O是椭圆的中心,A是椭圆短轴上的一个顶点,由于∠F1PF2=60°,则只需满足60°≤∠F1AF2即可,
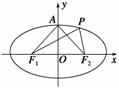 又△F1AF2是等腰三角形,且|AF1|=|AF2|,所以0°<∠F1F2A≤60°,
又△F1AF2是等腰三角形,且|AF1|=|AF2|,所以0°<∠F1F2A≤60°,
所以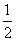 ≤cos∠F1F2A<1,
≤cos∠F1F2A<1,
又e=cos∠F1F2A,所以e的取值范围是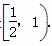 .
.
(2)证明 由(1)知mn=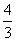 b2,
b2,
∴S△PF1F2=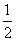 mnsin 60°=
mnsin 60°=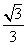 b2,
b2,
即△PF1F2的面积只与短轴长有关.

练习册系列答案
相关题目
 (x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________.
(x-1)与圆O:x2+y2=1在第一象限内交于点M,且l与y轴交于点A,则△MOA的面积等于________. .
. +
+ =8,求k的值.
=8,求k的值. +
+ =1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为
=1(m>0,n>0)的右焦点与抛物线y2=8x的焦点相同,离心率为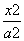 -
-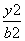 =1(a>0,b>0)的左、右焦点.若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( ).
=1(a>0,b>0)的左、右焦点.若在双曲线右支上存在点P,满足|PF2|=|F1F2|,且F2到直线PF1的距离等于双曲线的实轴长,则该双曲线的渐近线方程为( ). 时,切线MA的斜率为-
时,切线MA的斜率为-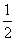 .
.