题目内容
已知圆x2+y2+x-6y+m=0和直线x+2y-3=0交于P,Q两点,且OP⊥OQ(O为坐标原点),求该圆的圆心坐标及半径.
解 法一 将x=3-2y,
代入方程x2+y2+x-6y+m=0,
得5y2-20y+12+m=0.
设P(x1,y1),Q(x2,y2),
则y1,y2满足条件:
y1+y2=4,y1y2=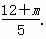 .
.
∵OP⊥OQ,∴x1x2+y1y2=0.
而x1=3-2y1,x2=3-2y2.
∵x1x2=9-6(y1+y2)+4y1y2=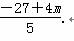 .
.
故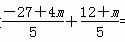 =0,解得m=3,
=0,解得m=3,
此时Δ=(-20)2-4×5×(12+m)=20(8-m)>0,圆心坐标为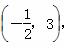 ,半径r=
,半径r=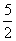 .
.
法二 如图所示,设弦PQ中点为M,且圆x2+y2+x-6y+m=0的圆心为O1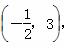 ,
,
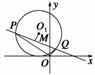 设M(x0,y0),P(x1,y1),Q(x2,y2),
设M(x0,y0),P(x1,y1),Q(x2,y2),
由法一知,y1+y2=4,x1+x2=-2,
∴x0=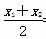 =-1,y0=
=-1,y0=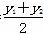 =2.
=2.
即M的坐标为(-1,2).
则以PQ为直径的圆可设为(x+1)2+
(y-2)2=r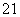 .
.
∵OP⊥OQ,∴点O在以PQ为直径的圆上.
∴(0+1)2+(0-2)2=r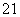 ,即r
,即r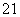 =5,|MQ|2=r
=5,|MQ|2=r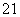 .
.
在Rt△O1MQ中,|O1Q|2=|O1M|2+|MQ|2.
∴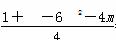 =
=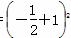 +(3-2)2+5.
+(3-2)2+5.
∴m=3,∴圆心坐标为 ,半径r=
,半径r=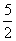 .
.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
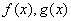 在[a,b]上连续,在(a,b)上可导且
在[a,b]上连续,在(a,b)上可导且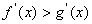 ,则当
,则当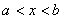 时,有( C )
时,有( C )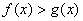 B.
B.
 D.
D.
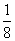 ,则这两条直线之间的距离的最大值和最小值分别为( ).
,则这两条直线之间的距离的最大值和最小值分别为( ).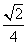 ,
,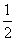 B.
B.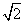 ,
,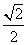 C.
C. -
- =1的一个焦点是(0,2),椭圆
=1的一个焦点是(0,2),椭圆 -
-