题目内容
18.在平面直角坐标系xOy中,已知成$\overrightarrow{OA}$=(-1,t),$\overrightarrow{OB}$=(2,2),若∠ABO=90°,则实数t的值为( )| A. | 1 | B. | -3 | C. | $\frac{1}{3}$ | D. | 5 |
分析 根据平面向量的坐标表示,用向量$\overrightarrow{OA}$、$\overrightarrow{OB}$表示出$\overrightarrow{AB}$,用向量垂直数量积为0列出方程求出t的值.
解答 解:平面直角坐标系xOy中,$\overrightarrow{OA}$=(-1,t),$\overrightarrow{OB}$=(2,2),
∴$\overrightarrow{AB}$=$\overrightarrow{OB}$-$\overrightarrow{OA}$=(3,2-t),
又∠ABO=90°,
∴$\overrightarrow{AB}$⊥$\overrightarrow{OB}$,
∴$\overrightarrow{AB}$•$\overrightarrow{OB}$=3×2+2(2-t)=0,
解得t=5.
故选:D.
点评 本题考查了平面向量的坐标表示与数量积运算问题,是基础题.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
9.函数y=sin(ωx+θ-$\frac{π}{6}$)的最小正周期为π,且其图象向左平移$\frac{π}{6}$单位得到的函数为奇函数,则θ的一个可能值是( )
| A. | $\frac{π}{3}$ | B. | -$\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | -$\frac{π}{6}$ |
13.圆的极坐标方程为ρ=2(cosθ+sinθ),则该圆的圆心极坐标是( )
| A. | $({1,\frac{π}{4}})$ | B. | $({\frac{1}{2},\frac{π}{4}})$ | C. | $(\sqrt{2},\frac{π}{4})$ | D. | $({2,\frac{π}{4}})$ |
10.二项式${({\sqrt{x}-\frac{1}{{\sqrt{x}}}})^{12}}$展开式中,x3的系数是( )
| A. | -495 | B. | -220 | C. | 495 | D. | 220 |
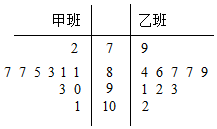 某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下:
某学校为了分析在一次数学竞赛中甲、乙两个班的数学成绩,分别从甲、乙两个班中随机抽取了10个学生的成绩,成绩的茎叶图如下: