题目内容
11．已知f（x）是奇函数，当x≥0时，f（x）=x（1-x），求f（x）的解析式．分析 根据f（x）为奇函数，可设x＜0，从而-x＞0，从而由条件得到f（-x）=-x（1+x）=-f（x），这样即可得出x＜0时的f（x）解析式，从而便可得出f（x）的解析式．
解答 解：f（x）是奇函数，设x＜0，-x＞0，则：
f（-x）=-x（1+x）=-f（x）；
∴f（x）=x（1+x）；
∴$f（x）=\left\{\begin{array}{l}{x（1-x）}&{x≥0}\\{x（1+x）}&{x＜0}\end{array}\right.$．
点评 考查奇函数的定义，对于奇函数，已知一区间上的解析式，而求其对称区间上解析式的方法，清楚分段函数的概念．
练习册系列答案
相关题目
1．
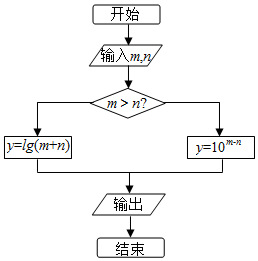若m=6，n=4，按照如图所示的程序框图运行后，输出的结果是（ ）
若m=6，n=4，按照如图所示的程序框图运行后，输出的结果是（ ）| A． | $\frac{1}{100}$ | B． | 100 | C． | 10 | D． | 1 |
已知椭圆E：$\frac{{x}^{2}}{{a}^{2}}$$+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的左右顶点A1，A2，椭圆上不同于A1，A2的点P，A1P，A2P两直线的斜率之积为-$\frac{4}{9}$，△PA1A2面积最大值为6．