题目内容
19.若$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-8),$\overrightarrow{a}$-$\overrightarrow{b}$=(-8,16),求$\overrightarrow{a}$$•\overrightarrow{b}$.分析 根据题意,设$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),由$\overrightarrow{a}$+$\overrightarrow{b}$与$\overrightarrow{a}$-$\overrightarrow{b}$的坐标,可得$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{y}_{1}+{y}_{2}=-8}\end{array}\right.$且$\left\{\begin{array}{l}{{x}_{1}-{x}_{2}=-8}\\{{y}_{1}-{y}_{2}=16}\end{array}\right.$,解可得向量$\overrightarrow{a}$与$\overrightarrow{b}$的坐标,进而由数量积的坐标计算公式计算可得答案.
解答 解:根据题意,设$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),
若$\overrightarrow{a}$+$\overrightarrow{b}$=(2,-8),$\overrightarrow{a}$-$\overrightarrow{b}$=(-8,16),
则有$\left\{\begin{array}{l}{{x}_{1}+{x}_{2}=2}\\{{y}_{1}+{y}_{2}=-8}\end{array}\right.$且$\left\{\begin{array}{l}{{x}_{1}-{x}_{2}=-8}\\{{y}_{1}-{y}_{2}=16}\end{array}\right.$;
解可得$\left\{\begin{array}{l}{{x}_{1}=-3}\\{{y}_{1}=4}\end{array}\right.$且$\left\{\begin{array}{l}{{x}_{2}=5}\\{{y}_{2}=-12}\end{array}\right.$,
即$\overrightarrow{a}$=(-3,4),$\overrightarrow{b}$=(5,-12),
则$\overrightarrow{a}$•$\overrightarrow{b}$=(-3)×5+4×(-12)=-63;
故$\overrightarrow{a}$•$\overrightarrow{b}$=-63.
点评 本题考查向量的坐标运算,注意先由向量的坐标运算求出向量$\overrightarrow{a}$与$\overrightarrow{b}$.

 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案| A. | 2$\sqrt{2}$ | B. | 3$\sqrt{2}$ | C. | 4$\sqrt{2}$ | D. | 5$\sqrt{2}$ |
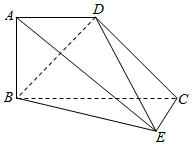 如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.
如图所示的几何体中,四边形ABCD为梯形,AD∥BC,AB⊥平面BEC,EC⊥CB.已知BC=2AD=2AB=2.