题目内容
9．函数f（x）=2ex的图象在点（0，f（0））处的切线方程为2x-y+2=0．分析 求出函数的导数，可得切线的斜率和切点，运用斜截式方程，可得切线的方程．
解答 解：函数f（x）=2ex的导数为f′（x）=2ex，
可得图象在点（0，f（0））处的切线斜率为k=2e0=2，
切点为（0，2），
则图象在点（0，f（0））处的切线方程为y=2x+2．
即为2x-y+2=0．
故答案为：2x-y+2=0．
点评 本题考查导数的运用：求切线方程，考查导数的几何意义，正确求导和运用斜截式方程是解题的关键，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
20．设向量$\vec a=（{cos{{45}°}，sin4{5°}}）$，$\vec b=（{cos{{15}°}，sin{{15}°}}）$，$\vec a•\vec b$=（ ）
| A． | $-\frac{{\sqrt{3}}}{2}$ | B． | $-\frac{1}{2}$ | C． | $\frac{1}{2}$ | D． | $\frac{{\sqrt{3}}}{2}$ |
1．已知函数f（x）=2ex，则（ ）
| A． | f′（x）=f（x）+2 | B． | f′（x）=f（x） | C． | f′（x）=3f（x） | D． | f′（x）=2f（x） |
18．已知λ∈R，向量$\overrightarrow a=（{3，λ}）\;，\;\overrightarrow b=（{λ-1\;，\;2}）$，则“λ=3”是“$\overrightarrow a∥\overrightarrow b$”的（ ）
| A． | 必要不充分条件 | B． | 充分不必要条件 | ||
| C． | 充分必要条件 | D． | 即不充分也不必要条件 |
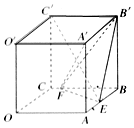如图，在棱长为2的正方体OABC-O′A′B′C′中，E，F分别是棱AB，BC上的动点．