题目内容
8.已知a∈R,f(x)=$\frac{a•{2}^{x}+a-2}{{2}^{x}+1}$(x∈R).(1)确定a的值,使f(x)为奇函数;
(2)当f(x)为奇函数时,对给定的正数k,求使f-1(x)>log2$\frac{1+x}{k}$成立的x的取值范围.
分析 (1)由f(x)+f(-x)=0,得$a+\frac{-2}{{2}^{x}+1}+a+\frac{-2}{{2}^{-x}+1}=0$,由此能求出当a=1时,f(x)是奇函数.
(2)f(x)=1+$\frac{-2}{{2}^{x}+1}$,令y=1+$\frac{-2}{{2}^{x}+1}$,得${f}^{-1}(x)=lo{g}_{2}\frac{1+x}{1-x}$,从而$lo{g}_{2}\frac{1+x}{1-x}$>$lo{g}_{2}\frac{1+x}{k}$,由此能求出使f-1(x)>log2$\frac{1+x}{k}$成立的x的取值范围.
解答 解:(1)∵a∈R,f(x)=$\frac{a•{2}^{x}+a-2}{{2}^{x}+1}$=a+$\frac{-2}{{2}^{x}+1}$,(x∈R).
∴$f(-x)=a+\frac{-2}{{2}^{-x}+1}$,
由f(x)+f(-x)=0,得$a+\frac{-2}{{2}^{x}+1}+a+\frac{-2}{{2}^{-x}+1}=0$,
整理,得2a=$\frac{2}{{2}^{x}+1}+\frac{2}{{2}^{-x}+1}$=2×$\frac{{2}^{-x}+1+{2}^{x}+1}{({2}^{x}+1)({2}^{-x}+1)}$=2,
解得a=1,∴当a=1时,f(x)是奇函数.
(2)由(1)得f(x)=1+$\frac{-2}{{2}^{x}+1}$,
令y=1+$\frac{-2}{{2}^{x}+1}$,得${2}^{x}+1=\frac{2}{1-y}$,
即${2}^{x}=\frac{1+y}{1-y}$,∴x=log2$\frac{1+y}{1-y}$,即${f}^{-1}(x)=lo{g}_{2}\frac{1+x}{1-x}$,
代入不等式,得$lo{g}_{2}\frac{1+x}{1-x}$>$lo{g}_{2}\frac{1+x}{k}$,∴k>1-x,
∵k>0,∴x>1-k,
∵函数的定义域是[-1,1],
∴使f-1(x)>log2$\frac{1+x}{k}$成立的x的取值范围为(1-k,1].
点评 本题考查实数值的求法,考查不等式的解法,考查反函数、对数不等式等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.

| A. | 过空间三点有且只有一个平面 | |
| B. | 若两个平面都和第三个平面垂直,则这两个平面平行 | |
| C. | 若两条直线都和第三条直线垂直,则这两条直线平行 | |
| D. | 垂直于同一平面的两条直线平行 |
| A. | -200 | B. | -120 | C. | 120 | D. | 200 |
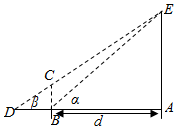 为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题:
为了培养学生的数学建模和应用能力,某校组织了一次实地测量活动,如图,假设待测量的树木AE的高度H(m),垂直放置的标杆BC的高度h=4m,仰角∠ABE=α,∠ADE=β(D,C,E三点共线),试根据上述测量方案,回答如下问题: