题目内容
14．已知函数f（x）=-x2+2ax+1，x∈[-1，2]，求f（x）的最大值（其中a∈R）．分析 求出函数的对称轴，通过讨论a的范围，求出函数的最大值即可．
解答 解：函数f（x）=-（x-a）2+a2+1，对称轴为x=a，函数的图象开口向下
当a≤-1时，函数在[-1，2]上单调减，此时x=-1，函数取到最大值-2a，
当-1＜a＜2时，此时x=a，函数取到最大值：a2+1，
当a≥2时，函数在[-1，2]上单调增，此时x=2，函数取到最大值4a-3．
点评 本题考查了二次函数的性质，考查分类讨论思想，是一道中档题．
练习册系列答案
相关题目
6．已知曲线C1：x2+y2-2y=1，曲线C2：xy=mx2-x，已知两条曲线有三个交点，则m的取值范围是（ ）
| A． | [-1，1] | B． | （-∞，-1）∪（1，+∞） | C． | {-1，1} | D． | （-1，1） |
3．已知双曲线$\frac{x^2}{m^2}-{y^2}=1（m＞0）$与抛物线y2=4x的准线交于A，B两点，O为坐标原点，若△AOB的面积等于1，则m=（ ）
| A． | $\sqrt{2}$ | B． | 1 | C． | $\frac{{\sqrt{2}}}{2}$ | D． | $\frac{1}{2}$ |
4．
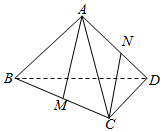空间四边形ABCD中，AB=BC=CD=DA=AC=BD=a，M，N分别是BC与AD的中点，设AM和CN所成角为α，则cosα的值为（ ）
空间四边形ABCD中，AB=BC=CD=DA=AC=BD=a，M，N分别是BC与AD的中点，设AM和CN所成角为α，则cosα的值为（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{3}{4}$ | D． | $\frac{1}{4}$ |