题目内容
4.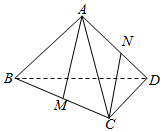 空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )
空间四边形ABCD中,AB=BC=CD=DA=AC=BD=a,M,N分别是BC与AD的中点,设AM和CN所成角为α,则cosα的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
分析 设O为MD的中点,连结ON、OC,则ON$\underset{∥}{=}$$\frac{1}{2}$AM,从而∠ONC或其补角为异面直线AM与CN所成的角.由此能求出cosα的值.
解答  解:如图,设O为MD的中点,连结ON、OC,则ON$\underset{∥}{=}$$\frac{1}{2}$AM.∴∠ONC或其补角为异面直线AM与CN所成的角.
解:如图,设O为MD的中点,连结ON、OC,则ON$\underset{∥}{=}$$\frac{1}{2}$AM.∴∠ONC或其补角为异面直线AM与CN所成的角.
∵ON=$\frac{1}{2}$AM=$\frac{\sqrt{3}}{4}$a,CN=$\frac{\sqrt{3}}{2}$a,
∴OC=$\sqrt{M{C}^{2}+M{O}^{2}}$=$\sqrt{\frac{1}{4}{a}^{2}+\frac{3}{16}{a}^{2}}$=$\frac{\sqrt{7}}{4}$a.
在△CON中,由余弦定理可得
cos∠CNO=$\frac{\frac{3}{4}{a}^{2}+\frac{3}{16}{a}^{2}-\frac{7}{16}{a}^{2}}{2•\frac{\sqrt{3}}{4}a•\frac{\sqrt{3}}{2}a}$=$\frac{2}{3}$.
∴cosα=$\frac{2}{3}$.
故选:A.
点评 本题考查角的余弦值的求法,是中档题,解题时要认真审题,注意异面直线所成角的余弦值的求法.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案
相关题目
15.已知动点P位于抛物线y2=4x上,定点An的坐标为($\frac{2}{3}$n,0)(n=1,2,3,4),则|$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$|+|$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$|的最小值为( )
| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | 2 |
16.在△ABC中,cosA=$\frac{3}{5}$,cosB=$\frac{4}{5}$,则sin(A+B)=( )
| A. | $\frac{7}{25}$ | B. | $\frac{9}{25}$ | C. | $\frac{16}{25}$ | D. | 1 |
13.设A、B、C、D四点都在同一个平面上,且$\overrightarrow{AC}$+4$\overrightarrow{DC}$=5$\overrightarrow{BC}$,则( )
| A. | $\overrightarrow{AB}$=4$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$=5$\overrightarrow{BD}$ | C. | $\overrightarrow{AC}$=4$\overrightarrow{BD}$ | D. | $\overrightarrow{AC}$=5$\overrightarrow{BD}$ |