题目内容
3.已知双曲线$\frac{x^2}{m^2}-{y^2}=1(m>0)$与抛物线y2=4x的准线交于A,B两点,O为坐标原点,若△AOB的面积等于1,则m=( )| A. | $\sqrt{2}$ | B. | 1 | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{1}{2}$ |
分析 根据条件求出抛物线的渐近线,联立方程求出A,B的坐标,根据三角形的面积建立方程进行求解即可.
解答 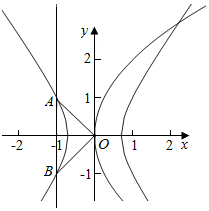 解:抛物线的准线为x=-1,
解:抛物线的准线为x=-1,
当x=-1时,$\frac{1}{{m}^{2}}$-y2=1,
即y2=$\frac{1}{{m}^{2}}$-1=$\frac{1-{m}^{2}}{{m}^{2}}$,0<m<1,
则y=±$\sqrt{\frac{1-{m}^{2}}{{m}^{2}}}$,
设A(-1,$\sqrt{\frac{1-{m}^{2}}{{m}^{2}}}$),B(-1,-$\sqrt{\frac{1-{m}^{2}}{{m}^{2}}}$),
则AB=2•$\sqrt{\frac{1-{m}^{2}}{{m}^{2}}}$,
则S=$\frac{1}{2}×$2$\sqrt{\frac{1-{m}^{2}}{{m}^{2}}}$×1=1,
即1-m2=m2,
则m2=$\frac{1}{2}$,
则m=$\frac{{\sqrt{2}}}{2}$,
故选:C
点评 本题主要考查双曲线和抛物线的应用,根据条件建立方程组关系是解决本题的关键.考查学生的计算能力.

练习册系列答案
相关题目
13.若函数y=f(x)对?x∈R恒有f(x+1)=f(x-1)=-f(1-x)成立,且y=f(x)不是常值函数,则函数y=f(x)在区间[-3,3]上的零点至少有( )
| A. | 3个 | B. | 4个 | C. | 6个 | D. | 7个 |
15.已知动点P位于抛物线y2=4x上,定点An的坐标为($\frac{2}{3}$n,0)(n=1,2,3,4),则|$\overrightarrow{P{A}_{1}}$+$\overrightarrow{P{A}_{2}}$|+|$\overrightarrow{P{A}_{3}}$+$\overrightarrow{P{A}_{4}}$|的最小值为( )
| A. | 4 | B. | $\frac{10}{3}$ | C. | $\frac{20}{3}$ | D. | 2 |
13.设A、B、C、D四点都在同一个平面上,且$\overrightarrow{AC}$+4$\overrightarrow{DC}$=5$\overrightarrow{BC}$,则( )
| A. | $\overrightarrow{AB}$=4$\overrightarrow{BD}$ | B. | $\overrightarrow{AB}$=5$\overrightarrow{BD}$ | C. | $\overrightarrow{AC}$=4$\overrightarrow{BD}$ | D. | $\overrightarrow{AC}$=5$\overrightarrow{BD}$ |