题目内容
设函数f(x)=lg(x2-x-6)的定义域为集合A,函数g(x)=
的定义域为集合B.已知α:x∈A∩B,β:x满足3x+p<0,且α是β的充分条件,求实数p的取值范围.
|
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:利用对数函数和根式函数分别得出函数f(x),g(x)的定义域,利用交集运算可得α:x∈A∩B,由β:x满足3x+p<0,可得x<-
.利用α是β的充分条件,即可得出.
| p |
| 3 |
解答:
解:要使函数f(x)=lg(x2-x-6)由意义,则x2-x-6>0,解得x>3或x<-2,
∴f(x)的定义域A=(-∞,-2)∪(3,+∞).
要使函数g(x)=
有意义,则
-1≥0,解得0<x≤6,∴g(x)的定义域B=(0,6].
α:x∈A∩B=(3,6],
β:x满足3x+p<0,∴x<-
.
∵α是β的充分条件,∴-
≥6,解得p≤-18.
∴f(x)的定义域A=(-∞,-2)∪(3,+∞).
要使函数g(x)=
|
| 6 |
| x |
α:x∈A∩B=(3,6],
β:x满足3x+p<0,∴x<-
| p |
| 3 |
∵α是β的充分条件,∴-
| p |
| 3 |
点评:本题考查了对数函数和根式函数的定义域、集合运算、充要条件、一元二次不等式的解法,考查了推理能力和计算能力,属于中档题.

练习册系列答案
相关题目
用反证法证明命题:“三角形的内角中至少有一个不大于60度”时,反设正确的是( )
| A、假设三内角都不大于60度 |
| B、假设三内角至多有一个大于60度 |
| C、假设三内角都大于60度 |
| D、假设三内角至多有两个大于60度 |
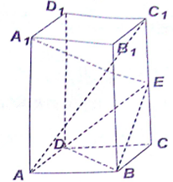 在正四棱柱ABCD-A11B1C1D1中,AA1=2AB=2,E为CC1的中点
在正四棱柱ABCD-A11B1C1D1中,AA1=2AB=2,E为CC1的中点