在正四棱柱ABCD-A11B1C1D1中.AA1=2AB=2.E为CC1的中点(1)求证:AC1∥平面BDE,(2)求证:A1E⊥平面BDE,(3)若F为BB1上的动点.使直线A1F与平面BDE所称角的正弦值是63.求DF的长．题目和参考答案——青夏教育精英家教网—

题目内容

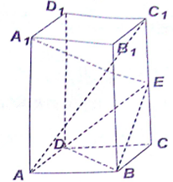在正四棱柱ABCD-A1₁B₁C₁D₁中，AA₁=2AB=2，E为CC₁的中点
（1）求证：AC₁∥平面BDE；
（2）求证：A₁E⊥平面BDE；
（3）若F为BB₁上的动点，使直线A₁F与平面BDE所称角的正弦值是

，求DF的长．

考点：直线与平面所成的角,直线与平面平行的判定,直线与平面垂直的判定

专题：平面向量及应用

分析：（1）连接AC，交BD于O，根据三角形中位线定理易得：OE∥AF，再由线面平行的判定定理，即可得到AC₁∥平面BDE．
（2）利用勾股定理求证△A₁BE和△A₁DE为直角三角形，再根据线面垂直的判定定理说明直线和平面垂直即可．
（3）建立空间直角坐标系，直线A₁F要和平面BDE有个交点，这个交点是未知的，可以设为G（x₀，y₀，z₀），则∠A₁GE是直线A₁F与平面BDE所成的角．看坐标中的x₀，y₀，z₀能否用其它的量来表示．G点是未知的，看有哪些条件来限制它．G点在平面BDE上，根据共面向量基本定理，存在一组实数λ，μ使

=λ

+μ

这样便得到第一个限制条件；G点在直线A₁F上，所以向量

A1G

与

A1F

共线，所以存在实数b使得

A1G

A1F

，这是找到的第二个条件．第三个条件就是，在Rt△A₁GE中，sin∠A₁GE=

A1E

A1G

，这样三个条件都找到，带入坐标进行运算即可．

解答：

证明：（1）如图，连接AC，交BD于O点，则O为AC的中点，连接EO；
∵E为CC₁的中点，
∴EO∥AC₁，
又∵EO?平面BED，AC₁?平面BED
∴AC₁∥平面BED，
（2）连接A₁B，A₁C₁，AA₁=2AB=2，E为CC₁的中点，
∴BE=

，A1E=

，A1D=

；
∴在△A₁BE中：BE2+A1E2=A1B2，则△A₁BE是直角三角形，∴A₁E⊥BE；
同理可证A₁E⊥DE；
∵BE∩DE=E；
∴A₁E⊥平面BDE．
（3）以DA所在直线为x轴，以DC所在直线为y轴，以DD₁所在的直线为z轴，建立如图所示的空间直角坐标系．
根据条件知道以下几个点坐标：
B（1，1，0），E（0，1，1），D（0，0，0），A₁（1，0，2），设F（1，1，m），设A₁F交平面BDE于G（x₀，y₀，z₀），连接A₁G，EG，则∠A₁GE 便是直线A₁F与平面BDE所成角；
先给出所用到的几个向量的坐标：

=(-1，-1，0)，

=（-1，0，1），

=（x₀-1，y₀-1，z₀），

A1G

=(x0-1，y0，z0-2)，

A1E

=(-1，1，-1)．
∵G在平面BDE上，∴存在一组实数λ，μ使

=λ

+μ

，带入坐标得：
（x₀-1，y₀-1，z₀）=λ（-1，-1，0）+μ（-1，0，1），所以得到：

x0-1=-λ-μ

y0-1=-λ