题目内容
13.在△ABC中,∠BAC=90°,AB=3,AC=4,若点D、E都在边BC上,且∠BAD=∠CAE=15°,则$\frac{BD•BE}{CD•CE}$=$\frac{9}{16}$.分析 根据条件便可由正弦定理分别得到$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①$\frac{BE}{sin75°}$=$\frac{3}{sin∠AEB}$②$\frac{CE}{sin15°}$=$\frac{4}{sin∠AEB}$③$\frac{CD}{sin75°}$=$\frac{4}{sin∠BDA}$④,而sin∠BDA=sin∠ADC,sin∠BEA=sin∠AEC,从而$\frac{①}{④}•\frac{②}{③}$得:$\frac{BD•BE}{CD•CE}$的值.
解答 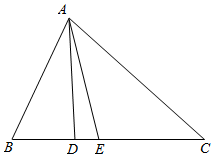 解:如图,由正弦定理得,$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①
解:如图,由正弦定理得,$\frac{BD}{sin15°}$=$\frac{3}{sin∠BDA}$①
$\frac{BE}{sin75°}$=$\frac{3}{sin∠AEB}$②
$\frac{CE}{sin15°}$=$\frac{4}{sin∠AEB}$③
$\frac{CD}{sin75°}$=$\frac{4}{sin∠BDA}$④
∴$\frac{①}{④}•\frac{②}{③}$得:$\frac{BD•BE}{CD•CE}$=$\frac{9}{16}$.
故答案为$\frac{9}{16}$.
点评 考查正弦定理以及三角函数的诱导公式:sin(π-α)=sinα,考查学生分析解决问题的能力,正确运用正弦定理是关键.

练习册系列答案
相关题目
3.已知集合A={x|x2-1=0},B={-1,2,5},则A∩B=( )
| A. | {-1,2} | B. | {-1} | C. | {-1,5} | D. | ∅ |
8.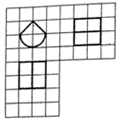 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,其中曲线部分是圆弧,则此几何体的表面积为( )| A. | 2+4$\sqrt{2}$+3π | B. | 2+4$\sqrt{2}$+5π | C. | 10+π | D. | 20+2π |
5.设a=0.30.1,b=log${\;}_{\frac{1}{3}}$$\frac{1}{5}$,c=log425,则a,b,c的大小关系是( )
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | c>b>a |
2. 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
 如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )
如图,将绘有函数f(x)=2sin(ωx+φ)(ω>0,$\frac{π}{2}$<φ<π)的部分图象的纸片沿x轴折成直二面角,若AB之间的空间距离为2$\sqrt{3}$,则f(-1)=( )| A. | -2 | B. | 2 | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |