题目内容
6.已知函数f(x)=$\frac{1}{2}$x2-(a+1)x+alnx+1.(Ⅰ)若x=3是f(x)的极值点,求f(x)的单调区间;
(Ⅱ)f(x)≥1恒成立,求a的取值范围.
分析 (Ⅰ)由于x=3是f(x)的极值点,则f′(3)=0求出a,进而求出f′(x)>0得到函数的增区间,求出f′(x)<0得到函数的减区间即可;
(Ⅱ)由于f(x)≥1恒成立,即x>0时,$\frac{1}{2}$x2-(a+1)x+alnx≥0恒成立,设g(x)=$\frac{1}{2}$x2-(a+1)x+alnx,求出函数的导数,分类讨论参数a,得到函数g(x)的最小值≥0,即可得到a的范围.
解答 解:(Ⅰ)f′(x)=x-(a+1)+$\frac{a}{x}$,
∵x=3是f(x)的极值点,
∴f′(3)=3-(a+1)+$\frac{a}{3}$=0,解得a=3,
当a=3时,f′(x)=$\frac{(x-1)(x-3)}{x}$,
当x变化时,
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 递增 | 极大值 | 递减 | 极小值 | 递增 |
(Ⅱ)要使得f(x)≥1恒成立,即x>0时,$\frac{1}{2}$x2-(a+1)x+alnx≥0恒成立,
设g(x)=$\frac{1}{2}$x2-(a+1)x+alnx,则g′(x)=x-(a+1)+$\frac{a}{x}$=$\frac{(x-1)(x-a)}{x}$,
(ⅰ)当a≤0时,由g′(x)<0得单减区间为(0,1),
由g′(x)>0得单增区间为(1,+∞),
故g(x)min=g(1)=-a-$\frac{1}{2}$≥0,得a≤-$\frac{1}{2}$;
( ii)当0<a<1时,由g′(x)<0得单减区间为(a,1),
由g′(x)>0得单增区间为(0,a),(1,+∞),
此时g(1)=-a-$\frac{1}{2}$<0,∴不合题意;
( iii)当a=1时,f(x)在(0,+∞)上单增,此时g(1)=-a-$\frac{1}{2}$<0,∴不合题意;
( iv)当a>1时,由g′(x)<0得单减区间为(1,a),
由g′(x)>0得单增区间为(0,1),(a,+∞),
此时g(1)=-a-$\frac{1}{2}$<0,∴不合题意.
综上所述:a≤-$\frac{1}{2}$时,f(x)≥1恒成立.
点评 本题考查利用导数研究函数的单调性及函数恒成立时所取的条件.考查考生的运算、推导、判断能力.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.已知F1(0,-1),F2(0,1)是椭圆的两个焦点,过F1的直线l交椭圆于M,N两点,若△MF2N的周长为8,则椭圆方程为( )
| A. | $\frac{{y}^{2}}{16}$+$\frac{{x}^{2}}{15}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{15}$=1 | C. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{y}^{2}}{4}$+$\frac{{x}^{2}}{3}$=1 |
9.如图所示是一个几何体的三视图,则这个几何体外接球的体积为( )
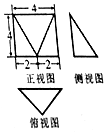

| A. | 36π | B. | $\frac{64\sqrt{2}}{3}$π | C. | 8$\sqrt{6}$π | D. | $\frac{8}{3}$π |
18.某香料加工厂生产“沉鱼落雁”和“国色天香”两种香料,已知生产两种香料每吨所需的原材料A,B,C的数量和一周内可用资源数量如下表所示:
如果“沉鱼落雁”每吨的利润为400元,“国色天香”每吨的利润为300元,那么应如何安排生产,才能使香料加工厂每周的利润最大?并求出最大利润.
| 原材料 | 沉鱼落雁(吨) | 国色天香(吨) | 可用资源数量(吨) |
| A | 3 | 2 | 20 |
| B | 3 | 1 | 20 |
| C | 2 | 5 | 25 |
15.在平面直角坐标系中,“直线ax+y-1=0与直线x+ay+2=0平行”是“a=1”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 非充分非必要条件 |