题目内容
11.设函数f(x)的定义域为R,f(x)=$\left\{\begin{array}{l}{-x,-1≤x≤0}\\{{3}^{x}-1,0<x<1}\end{array}\right.$,且对任意的x∈R都有f(x+1)=-$\frac{1}{f(x)}$,若在区间[-5,1]上函数g(x)=f(x)-mx+m恰有5个不同零点,则实数m的取值范围是( )| A. | [-$\frac{1}{4}$,-$\frac{1}{6}$) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$] | C. | (-$\frac{1}{6}$,0] | D. | (-$\frac{1}{2}$,-$\frac{1}{6}$] |
分析 求出f(x)的周期,作出f(x)的函数图象,令y=mx-m与f(x)在[-5,1]上的图象有5个交点,即可求出m的范围.
解答 解:∵f(x+1)=-$\frac{1}{f(x)}$,∴f(x+2)=-$\frac{1}{f(x+1)}$,
∴f(x)=f(x+2),即f(x)的周期为2.
作出f(x)在[-5,1]上的函数图象如图所示: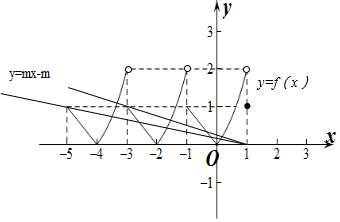
令g(x)=0得f(x)=mx-m,
则直线y=mx-m与f(x)在[-5,1]上有5个交点.
当直线y=mx-m过点(-3,1)时,直线y=mx-m与f(x)在[-5,1]上恰好有5个交点,
此时-3m-m=1,即m=-$\frac{1}{4}$,
当直线y=mx-m过点(-5,1)时,直线y=mx-m与f(x)在[-5,1]上恰好有6个交点,
此时-5m-m=1,即m=-$\frac{1}{6}$.
∴-$\frac{1}{4}$≤m<-$\frac{1}{6}$.
故选A.
点评 本题考查了函数的周期性应用,函数图象与函数零点的关系,属于中档题.

练习册系列答案
相关题目
7.若对?m,n∈R,有g(m+n)=g(m)+g(n)-3,求$f(x)=\frac{{x\sqrt{1-{x^2}}}}{{{x^2}+1}}+g(x)$的最大值与最小值之和是( )
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
20.已知直线l:ax+by-2=0平分圆x2+y2-6x-4y-12=0,若a,b均为正数,则$\frac{3}{a}$+$\frac{2}{b}$的最小值是( )
| A. | 25 | B. | 12 | C. | $\frac{25}{2}$ | D. | 9 |
1.设函数f(x)=(ex-1)•(x-1)2则( )
| A. | f(x)在x=1处取到极小值 | B. | f(x)在x=1处取到极大值 | ||
| C. | f(x)在x=-1处取到极小值 | D. | f(x)在x=-1处取到极大值 |