题目内容
7.若对?m,n∈R,有g(m+n)=g(m)+g(n)-3,求$f(x)=\frac{{x\sqrt{1-{x^2}}}}{{{x^2}+1}}+g(x)$的最大值与最小值之和是( )| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
分析 构造h(x)=g(x)-3,根据函数奇偶性的定义可判定函数h(x)为奇函数,利用奇函数图象的性质即可求出答案.
解答 解:∵?m,n∈R,有g(m+n)=g(m)+g(n)-3,
∴令m=n=0时,g(0)=g(0)+g(0)-3,
∴g(0)=3,
令m=-n时,g(0)=g(-n)+g(n)-3,
∴g(x)+g(-x)=6,
令h(x)=g(x)-3,则h(x)+h(-x)=0即h(x)为奇函数,
奇函数的图象关于原点对称,它的最大值与最小值互为相反数,∴g(x)max+g(-x)min=6,
设F(x)=$\frac{x\sqrt{1-{x}^{2}}}{{x}^{2}+1}$,则F(-x)=-F(x),函数为奇函数,最大值与最小值之和为0,
∴.$f(x)=\frac{{x\sqrt{1-{x^2}}}}{{{x^2}+1}}+g(x)$的最大值与最小值之和是6.
故选B.
点评 本题考查了抽象函数及其应用,主要考查了函数的性质的应用,本题主要考查了利用赋值法求解抽象函数的函数值,解决本题的关键是恰当构造奇函数.属于中档题.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
15.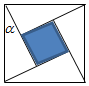 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
( )
 “勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是
“勾股定理”在西方被称为“毕达哥拉斯定理”,三国时期吴国的数学家赵爽创制了一幅“勾股圆方图”,用数形结合的方法给出了勾股定理的详细证明.如图所示的“勾股圆方图”中,四个相同的直角三角形与中间的小正方形拼成一个边长为2的大正方形,若直角三角形中较小的锐角$α=\frac{π}{6}$,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内的概率是( )
| A. | $1-\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{4-\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
19.已知函数f(x)=sinωx-$\sqrt{3}$cosωx(ω>0)在(0,π)上有且只有两个零点,则实数ω的取值范围为( )
| A. | $({0,\frac{4}{3}}]$ | B. | $({\frac{4}{3},\frac{7}{3}}]$ | C. | $({\frac{7}{3},\frac{10}{3}}]$ | D. | $({\frac{10}{3},\frac{13}{3}}]$ |
16.设θ∈R,“sinθ=cosθ“是“cos2θ=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
11.设函数f(x)的定义域为R,f(x)=$\left\{\begin{array}{l}{-x,-1≤x≤0}\\{{3}^{x}-1,0<x<1}\end{array}\right.$,且对任意的x∈R都有f(x+1)=-$\frac{1}{f(x)}$,若在区间[-5,1]上函数g(x)=f(x)-mx+m恰有5个不同零点,则实数m的取值范围是( )
| A. | [-$\frac{1}{4}$,-$\frac{1}{6}$) | B. | (-$\frac{1}{2}$,-$\frac{1}{4}$] | C. | (-$\frac{1}{6}$,0] | D. | (-$\frac{1}{2}$,-$\frac{1}{6}$] |
 在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.
在斜三棱柱ABC-A1B1C1中,侧面AC1⊥平面ABC,$A{A_1}=\sqrt{2}a$,A1C=CA=AB=a,AB⊥AC,D是AA1的中点.