题目内容
设函数f(x),g(x)的定义域分别为F,G,且F⊆G,若对任意x∈F,都有g(x)=f(x),则称g(x)为f(x)在G上的一个“延拓函数”,已知函数f(x)=2x(x≤0),若g(x)为f(x)在R上延拓函数,且g(x)是偶函数,则函数g(x)的解析式是 .
考点:函数解析式的求解及常用方法
专题:函数的性质及应用
分析:由题意函数f(x)=2x(x≤0),g(x)为f(x)在R上一个延拓函数,求出g(x),然后利用偶函数推出函数g(x)的解析式.
解答:
解:f(x)=2x(x≤0),
g(x)为f(x)在R上的一个延拓函数,
则当x∈(-∞,0]时,
g(x)=f(x)=2x,
g(x)是偶函数
当x>0时,
g(x)=g(-x)=2-x,
综上g(x)=2-|x|.
故答案为:2-|x|.
g(x)为f(x)在R上的一个延拓函数,
则当x∈(-∞,0]时,
g(x)=f(x)=2x,
g(x)是偶函数
当x>0时,
g(x)=g(-x)=2-x,
综上g(x)=2-|x|.
故答案为:2-|x|.
点评:本题考查求指数函数解析式,奇函数的性质,考查计算能力,推理能力,是基础题.创新题型.

练习册系列答案
相关题目
下列哪组中的函数f(x)与g(x)相等( )
A、f(x)=x2,g(x)=(
| ||||||
B、f(x)=x+1,g(x)=
| ||||||
C、f(x)=x,g(x)=
| ||||||
D、f(x)=
|
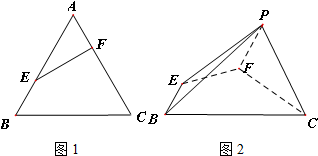 在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC=
在图1等边三角形ABC中,AB=2,E是线段AB上的点(除点A外),过点E作EF⊥AC于点F,将△AEF 沿EF折起到△PEF(点A与点P重合,如图2),使得∠PFC= 如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为
如图,正六边形ABCDEF的两个顶点A,D为椭圆的两个焦点,其余四个顶点在椭圆上,则该椭圆的离心率为