题目内容
已知全集R,集合A={x||x-3|>6},B={x||x|>a,a∈N+},当a为何值时,
(1)A是B的充分而不必要条件;
(2)A是B的必要而不充分条件;
(3)A是B的充要条件.
(1)A是B的充分而不必要条件;
(2)A是B的必要而不充分条件;
(3)A是B的充要条件.
考点:函数奇偶性的性质
专题:集合思想,不等式的解法及应用
分析:先解出集合A与集合B,再利用充分而不必要条件;必要而不充分条件;充要条件的定义
分别转化为B?A,A?B,A=B的集合关系,最后利用数轴判断即可得出a的值.
分别转化为B?A,A?B,A=B的集合关系,最后利用数轴判断即可得出a的值.
解答:
解:集合A={x||x-3|>6},B={x||x|>a,a∈N+},
解得:A={x|x>9或x<-3},B={x|x>a或x<-a,a∈N+},
(1):∵A是B的充分而不必要条件,∴B?A,
可得-3≤-a<9,a∈N+,
即1≤a≤3
(2):∵A是B的必要而不充分条件,∴A?B,可得a≥9,
即实数a≥9.
(3):∵A是B的充要条件,∴A=B,可得-a=-3且a=9,
可得不可能有这样a∈N+的存在
解得:A={x|x>9或x<-3},B={x|x>a或x<-a,a∈N+},
(1):∵A是B的充分而不必要条件,∴B?A,
可得-3≤-a<9,a∈N+,
即1≤a≤3
(2):∵A是B的必要而不充分条件,∴A?B,可得a≥9,
即实数a≥9.
(3):∵A是B的充要条件,∴A=B,可得-a=-3且a=9,
可得不可能有这样a∈N+的存在
点评:本题考察了不等式,集合,充要条件的关系,属于基本知识的考察,运用好数轴是关键.

练习册系列答案
相关题目
如图是导函数y=f′(x)的图象,那么函数y=f(x)在区间[a,b]内的极值点有( )
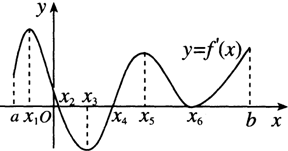

| A、0 | B、1 | C、2 | D、3 |

 已知函数f(x)=
已知函数f(x)=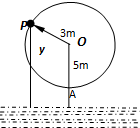 如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=
如图为一半径为3米的水轮,水轮圆心O距水面5米,已知水轮每分钟逆时针转6圈,水轮上的固定点P到水面距离y(米)与时间x(秒)满足关系式y=Asin(ωx+φ)+b的函数形式,当水轮开始转动时P点位于距离水面最近的A点处,则A=