题目内容

函数f（x）=ex-ex的单调增区间为
 
．
考点：利用导数研究函数的单调性
专题：导数的综合应用
分析：求出函数的导数，令f′（x）≤0，解出即可．
解答： 解：函数f（x）=ex-ex
则f′（x）=ex-e，
令f′（x）＞0，解得x＞1．
∴f（x）的单调减区间为（1，∞）．
故答案为：（1，+∞）．
点评：本题考查了利用导数研究函数的单调性，属于基本知识的考查．
练习册系列答案
相关题目
如果实数x、y满足条件
x-y+1≥0
y+1≥0
x+y+1≤0
，那么z=4x•2-y的最大值为（　　）
A、1
B、2
C、
1
2
D、
1
4
设复数z1=1+i，z2=2+xi，（x∈R），若z1•z2∈R，则x的值等于
 
．
已知集合A={3，5，6，8}，B={1，3，5}，那么A∪B等于（　　）
A、{1，3，5，6，8}
B、{6，8}
C、{3，5}
D、{1，6，8}
已知2sinα-cosα=0，求
1+2sin(π-α)cos(-2π-α)
sin2(-α)-sin2(
5
2
π-α)
的值．
如图，DC垂直平面ABC，∠BAC=90°，AC=
1
2
BC=kCD，点E在BD上，且BE=3ED．
（1）求证：AE⊥BC；
（2）若二面角B-AE-C的大小为120°，求k的值．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
5
3
，设其左、右焦点分别为F1，F2，上顶点为B1，且F2到直线B1F1的距离为
4
5
3
．
（Ⅰ）求椭圆的方程；
（Ⅱ）过点（2，0）作直线与椭圆交于A，B两点，O是坐标原点，是否存在这样的直线，使得|
OA
+
OB
|=|
OA
-
OB
|？若存在，求出直线的方程，若不存在，试说明理由．
已知函数f（x）=lnx+
1-x
a(1+x)
，其中a为不为零的常数．
（Ⅰ）若f（x）在点（1，0）处的切线过点（2，-1），求实数a的值；
（Ⅱ）当a=1时，若存在x1，x2∈[1，e2]使得f（x1）-f（x2）≥M成立，求满足条件的最大整数M；
（Ⅲ）若f（x）无极值，求实数a的取值范围．
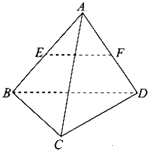如图，四面体ABCD的每条棱长都等于2，点E，F分别为棱AB，AD的中点，则|
AB
+
BC
|=
 
，|
BC
-
EF
|=
 
，
EF
与
AC
所成的角为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网