题目内容
7.函数f(x)=2x+cosx在x=$\frac{π}{2}$处的切线与坐标轴围成三角形面积为( )| A. | $\frac{π^2}{8}$ | B. | $\frac{π^2}{24}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
分析 求函数的导数,利用导数的几何意义进行求解即可.
解答 函数的导数f′(x)=2-sinx,
则在x=$\frac{π}{2}$处的切线斜率k=f′($\frac{π}{2}$)=2-sin$\frac{π}{2}$=2-1=1,
即切线斜率k=1,f($\frac{π}{2}$)=2×$\frac{π}{2}$+cos$\frac{π}{2}$=π,
即切点坐标为($\frac{π}{2}$,π),
则切线方程为y-π=x-$\frac{π}{2}$,
即y=x+$\frac{π}{2}$,
直线与坐标轴的两个交点为(0,$\frac{π}{2}$),(-$\frac{π}{2}$,0),
则对应的三角形的面积S=$\frac{1}{2}$×$\frac{π}{2}$×$\frac{π}{2}$=$\frac{π^2}{8}$,
故选:A
点评 本题主要考查函数切线的求解以及三角形的面积的计算,根据导数的几何意义求出切线方程是解决本题的关键.

练习册系列答案
相关题目
17.数列{an}是等差数列,且a1>0,若a1008+a1009>0,a1008•a1009<0同时成立,则使得Sn>0成立的n的最大值为( )
| A. | 2016 | B. | 2017 | C. | 2018 | D. | 2019 |
18.如图是一个算法的程序框图,当输入x的值为3时,输出y的结果恰好是$\frac{1}{3}$,则?处的关系式可以是( )
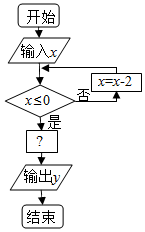

| A. | y=x2 | B. | y=3-x | C. | y=3x | D. | y=x${\;}^{\frac{1}{3}}$ |
2.下列命题中,真命题是( )
| A. | ?x∈R,x2≤x-2 | |
| B. | ?x∈R,2x>2-x2 | |
| C. | 函数f(x)=$\frac{1}{x}$为定义域上的减函数 | |
| D. | “被2整除的整数都是偶数”的否定是“至少存在一个被2整除的整数不是偶数” |
12.集合A={x|x≤a},B={x|x2-5x<0},若A∩B=B,则a的取值范围是( )
| A. | a≥5 | B. | a≥4 | C. | a<5 | D. | a<4 |
16.若(z-1)2=-1,则z的值为( )
| A. | 1+i | B. | 1±i | C. | 2+i | D. | 2±i |