题目内容
要得到函数y=2cos（2x+
）的图象，只需将函数y=sin2x+
cos2x的图象（ ）
| π |
| 3 |
| 3 |
A、向左平移
| ||
B、向右平移
| ||
C、向右平移
| ||
D、向左平移
|
考点：函数y=Asin（ωx+φ）的图象变换
专题：三角函数的图像与性质
分析：由两角差的余弦把y=sin2x+
cos2x化积，然后看x发生如何变化得y=2cos（2x+
）．
| 3 |
| π |
| 3 |
解答：
解：y=sin2x+
cos2x=2(
sin2x+
cos2x)=2cos(2x-
)．
又数y=2cos（2x+
）=2cos(2x+
+
-
)=2cos(2x+
-
)=2cos[2(x+
)-
]，
∴只需要将y=sin2x+
cos2x的图象向左平移
个单位，即可得到y=2cos（2x+
）的图象．
故选：A．
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| π |
| 6 |
又数y=2cos（2x+
| π |
| 3 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 6 |
| π |
| 4 |
| π |
| 6 |
∴只需要将y=sin2x+
| 3 |
| π |
| 4 |
| π |
| 3 |
故选：A．
点评：本题考查了y=Asin（ωx+φ）型函数的图象，考查了两角和与差的三角函数，是中档题．
练习册系列答案
名校课堂系列答案
相关题目
已知变量x，y满足约束条件
，则z=2x+y的最大值是（ ）
|
| A、-3 | ||
B、
| ||
| C、3 | ||
| D、5 |
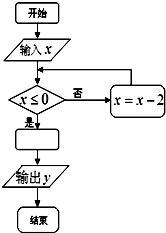如图是一个算法程序框图，当输入的x值为3时，输出的结果恰好是| 1 |
| 3 |
A、y=x -
| ||
B、y=x
| ||
| C、y=3-x | ||
| D、y=3x |
如果复数（1+bi）（2+i）是纯虚数，则|
|的值为（ ）
| 2b+3i |
| 1+bi |
| A、2 | ||
B、
| ||
| C、5 | ||
| D、15 |
不等式
＜0的解集是（ ）
| x(x-1)2 |
| x+1 |
| A、{x|-1＜x＜1} |
| B、{x|0＜x＜1} |
| C、{-1＜x＜0} |
| D、{x|x＞1或-1＜x＜0} |
设圆锥曲线C的两个焦点分别为F1、F2，若曲线C上存在点P满足|PF1|：|F1F2|：|PF2|=4：3：2，则曲线C的离心率等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|