题目内容
设函数f(x)=ax-ex,a∈R,e为自然对数的底数.
(1)若函数f(x)存在两个零点,求a的取值范围;
(2)若对任意x∈R,a>0.f(x)≤a2-ka恒成立,求实数k的取值范围.
(1)若函数f(x)存在两个零点,求a的取值范围;
(2)若对任意x∈R,a>0.f(x)≤a2-ka恒成立,求实数k的取值范围.
考点:利用导数研究函数的单调性,函数零点的判定定理
专题:计算题,导数的综合应用
分析:(1)求导f′(x)=a-ex,分a>0与a<0讨论,从而可得当a>0时,f(x)在x=lna处取得最大值f(lna)=alna-a,从而可得f(lna)=alna-a>0,从而解a;
(2)由题意,对任意x∈R,a>0.f(x)≤a2-ka恒成立可化为k≤a+1-lna恒成立,令g(a)=a+1-lna,从而化为最值问题.
(2)由题意,对任意x∈R,a>0.f(x)≤a2-ka恒成立可化为k≤a+1-lna恒成立,令g(a)=a+1-lna,从而化为最值问题.
解答:
解:(1)f′(x)=a-ex.
当a≤0时,f′(x)<0,f(x)在R上单调递减,最多存在一个零点,不满足条件;
当a>0时,由f′(x)=0解得x=lna,当x>lna时,f′(x)<0,当x<lna时,f′(x)>0.
故f(x)在x=lna处取得最大值f(lna)=alna-a,
∵f(x)存在两个零点,
∴f(lna)=alna-a>0,
∴a>e,
即a的取值范围是(e,+∞);
(2)由(Ⅰ)知f(x)≤alna-a,故只需alna-a≤a2-ka,
即k≤a+1-lna.
令g(a)=a+1-lna,
g′(a)=1-
,
当a>1时,g′(a)>0;当a<1时,g′(a)<0.
故g(a)在a=1处取得最小值2,则k≤2,
即k的取值范围是(-∞,2].
当a≤0时,f′(x)<0,f(x)在R上单调递减,最多存在一个零点,不满足条件;
当a>0时,由f′(x)=0解得x=lna,当x>lna时,f′(x)<0,当x<lna时,f′(x)>0.
故f(x)在x=lna处取得最大值f(lna)=alna-a,
∵f(x)存在两个零点,
∴f(lna)=alna-a>0,
∴a>e,
即a的取值范围是(e,+∞);
(2)由(Ⅰ)知f(x)≤alna-a,故只需alna-a≤a2-ka,
即k≤a+1-lna.
令g(a)=a+1-lna,
g′(a)=1-
| 1 |
| a |
当a>1时,g′(a)>0;当a<1时,g′(a)<0.
故g(a)在a=1处取得最小值2,则k≤2,
即k的取值范围是(-∞,2].
点评:本题考查了导数的综合应用及函数的零点及恒成立问题,属于中档题.

练习册系列答案
相关题目
设集合A={x|x2-4x<0},B={x|x-2>0},则A∩B=( )
| A、(0,2) |
| B、(0,4) |
| C、(4,+∞) |
| D、(2,4) |
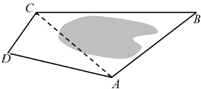 如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为
如图为了测量A,C两点间的距离,选取同一平面上B,D两点,测出四边形ABCD各边的长度(单位:km):AB=5,BC=8,CD=3,DA=5,如图所示,且A、B、C、D四点共圆,则AC的长为