��Ŀ����
11��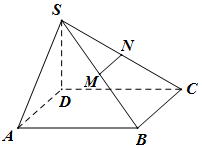 ��֪����S-ABCD�ĵ���Ϊƽ���ı��Σ���SD����ABCD��AB=2AD=2SD����DCB=60�㣬M��N�ֱ�ΪSB��SC�е㣬��MN��ƽ��MNPQ�ֱ����߶�CD��AB�ཻ�ڵ�P��Q��
��֪����S-ABCD�ĵ���Ϊƽ���ı��Σ���SD����ABCD��AB=2AD=2SD����DCB=60�㣬M��N�ֱ�ΪSB��SC�е㣬��MN��ƽ��MNPQ�ֱ����߶�CD��AB�ཻ�ڵ�P��Q��������ͼ������ƽ��MNPQ��ʹ��MNPQ����SAD����Ҫ��֤������
������$\overrightarrow{AQ}=��\overrightarrow{AB}$���Ƿ����ʵ���ˣ�ʹ�����M-PQ-B��ƽ��Ǵ�СΪ60�㣿�����ڣ�����Ħ�ֵ���������ڣ���˵�����ɣ�
���� ����Q��AB���е㻭ͼ���ɣ�
����֤��AD��BD����DΪԭ�㣬ֱ��DAΪx�ᣬֱ��DBΪy�ᣬֱ��DSΪz�Ὠ���ռ�ֱ������ϵ�����ƽ��ķ���������ABCD�ķ����������ö����M-PQ-BΪ60�㣬����˼��ɣ�
��� �⣺������ͼ��Q��AB���е㣨��NP��PQδ�������ߣ������֣�����4�֣�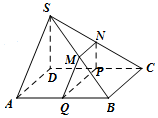
������ƽ���ı���ABCD�У���AB=2AD=4����DCB=60�㣬���������Ҷ������$BD=2\sqrt{3}$����AB2=AD2+BD2������AD��BD��������5�֣�
��DΪԭ�㣬ֱ��DAΪx�ᣬֱ��DBΪy�ᣬֱ��DSΪz�Ὠ���ռ�ֱ������ϵ��
��$A��{2��0��0}����B��{0��2\sqrt{3}��0}����S��{0��0��2}����M��{0��\sqrt{3}��1}��$��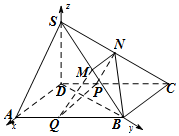
��$\overrightarrow{AQ}=��\overrightarrow{AB}$����Q��x��y��z������$��{x-2��y��z}��=�ˣ�{-2��2\sqrt{3}��0}��$
��$Q��{2-2�ˣ�2\sqrt{3}�ˣ�0}��$����7�֣�
��ƽ��ķ�����Ϊ$\overrightarrow n=��{x��y��z}��$
��$\left\{{\begin{array}{l}{\overrightarrow n•\overrightarrow{AD}=0}\\{\overrightarrow n•\overrightarrow{MQ}=0}\end{array}}\right.$��$\overrightarrow n=��{0��1��\sqrt{3}��{2��-1}��}��$������9�֣�
��֪��ABCD�ķ�����Ϊ$\overrightarrow m=��{0��0��1}��$
Ҫʹ�����M-PQ-BΪ60�㣬����$cos{60��}=\frac{1}{2}=\frac{{|{\overrightarrow m\overrightarrow{•n}}|}}{{|{\overrightarrow m}||{\overrightarrow n}|}}=\frac{{|{\sqrt{3}��{2��-1}��}|}}{{\sqrt{1+3{{��{2��-1}��}^2}}}}$���$��=\frac{1}{3}���=\frac{2}{3}$������11�֣�
��ͼ��֪��Ҫʹ�����M-PQ-BΪ60�㣬��$��=\frac{1}{3}$����12�֣�
���� ���⿼��ƽ����ƽ��ƽ�е��жϣ�����ǵ�ƽ��ǵ�����Ӧ�ã�������������Լ�ת��˼�룮

 ��У����ϵ�д�
��У����ϵ�д�| A�� | 10 | B�� | 11 | C�� | 12 | D�� | 13 |
| A�� | $-\frac{4}{5}+\frac{3}{5}i$ | B�� | $-\frac{3}{5}+\frac{4}{5}i$ | C�� | $-\frac{1}{2}+\frac{3}{2}i$ | D�� | $-\frac{1}{2}-\frac{3}{2}i$ |
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��ֱ�Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
| A�� | 1 | B�� | $\sqrt{2}$ | C�� | $\sqrt{3}$ | D�� | 2 |
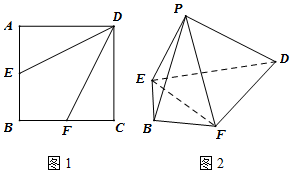 ��ͼ1���߳�Ϊ4��������ABCD�У���E��F�ֱ��DZ�AB��BC���е㣬����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�P��ͼ2��
��ͼ1���߳�Ϊ4��������ABCD�У���E��F�ֱ��DZ�AB��BC���е㣬����AED����DCF�ֱ���DE��DF����ʹA��C�����غ��ڵ�P��ͼ2��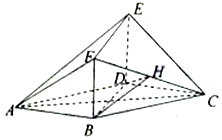 ��ͼ���ڶ�����ABCDEF�У�ƽ��BDEF��ƽ��ABCD���ı���ABCD�����Σ��ı���BDEF�Ǿ��Σ�BD=2BF��H��CF���е㣮
��ͼ���ڶ�����ABCDEF�У�ƽ��BDEF��ƽ��ABCD���ı���ABCD�����Σ��ı���BDEF�Ǿ��Σ�BD=2BF��H��CF���е㣮