题目内容
19.设i为虚数单位,则复数$z=\frac{1-i}{1+i}$的模为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 利用复数的运算法则、模的计算公式即可得出.
解答 解:复数$z=\frac{1-i}{1+i}$=$\frac{(1-i)^{2}}{(1+i)(1-i)}$=$\frac{-2i}{2}$=-i,
∴|z|=1.
故选:A.
点评 本题考查了复数的运算法则、模的计算公式,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
7.已知平面α⊥平面β,直线m,n均不在平面α、β内,且m⊥n,则( )
| A. | 若m⊥β,则n∥β | B. | 若n∥β,则m⊥β | C. | 若m⊥β,则n⊥β | D. | 若n⊥β,则m⊥β |
11.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左,右焦点分别为F1,F2,双曲线上一点P满足PF2⊥x轴.若|F1F2|=12,|PF2|=5,则该双曲线的离心率为( )
| A. | 3 | B. | $\frac{3}{2}$ | C. | $\frac{12}{5}$ | D. | $\frac{13}{12}$ |
9.已知集合A={x|y=log2(3-x)},B={x||2x-1|>1},则A∩B=( )
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|x<0或0<x<3} | D. | {x|x<0或1<x<3} |
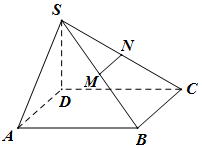 已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q.
已知四棱锥S-ABCD的底面为平行四边形,且SD⊥面ABCD,AB=2AD=2SD,∠DCB=60°,M,N分别为SB,SC中点,过MN作平面MNPQ分别与线段CD,AB相交于点P,Q.