题目内容
12.已知函数y=f(x)(x∈I),对函数y=g(x)(x∈I),定义g(x)关于f(x)的“对称函数”为函数y=h(x),x∈I.即y=h(x),x∈I满足对任意x∈I,两点(x,h(x)),(x,g(x))关于点(x,f(x))对称.若h(x)是$g(x)=\sqrt{4-{x^2}}$关于f(x)=3x+m的对称函数,且h(x)>g(x)恒成立,则实数m的取值范围是(2$\sqrt{10}$,+∞).分析 根据对称函数的定义,将不等式恒成立转化为直线和圆的位置关系,数形结合得结论.
解答 解:根据“对称函数”的定义可知,$\frac{h(x)+\sqrt{4-{x}^{2}}}{2}$=3x+m,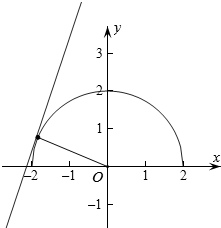
即h(x)=6x+2m-$\sqrt{4-{x}^{2}}$,
若h(x)>g(x)恒成立,
则等价为6x+2m-$\sqrt{4-{x}^{2}}$>$\sqrt{4-{x}^{2}}$,
即3x+m>$\sqrt{4-{x}^{2}}$恒成立,
设y1=3x+m,y2=$\sqrt{4-{x}^{2}}$,
作出两个函数对应的图象如图,
当直线和上半圆相切时,圆心到直线的距离d=$\frac{|m|}{\sqrt{10}}$=2,
即|m|=2$\sqrt{10}$,
∴m=2$\sqrt{10}$或-2$\sqrt{10}$,(舍去),
即要使h(x)>g(x)恒成立,
则m>2$\sqrt{10}$,
即实数m的取值范围是(2$\sqrt{10}$,+∞),
故答案为:(2$\sqrt{10}$,+∞).
点评 本题主要考查对称函数的定义的理解,以及不等式恒成立的证明,利用直线和圆的位置关系是解决本题的关键,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.已知函数f(x)=$\frac{x}{{e}^{x}}$(e是对自然对数的底数),则其导函数f'(x)=( )
| A. | $\frac{1+x}{{e}^{x}}$ | B. | $\frac{1-x}{{e}^{x}}$ | C. | 1+x | D. | 1-x |
3.已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有$f[{f(x)+{{log}_{\frac{1}{3}}}x}]=4$,且方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解,则实数a的取值范围是( )
| A. | 0<a≤5 | B. | a<5 | C. | 0<a<5 | D. | a≥5 |
20.已知$f(x)=\left\{\begin{array}{l}x+1,({0≤x<1})\\{2^x}-\frac{1}{2},({x≥1})\end{array}\right.$,设a>b≥0,若f(a)=f(b),则b•f(a)的取值范围是( )
| A. | (1,2] | B. | $({\frac{3}{4},2}]$ | C. | $[{\frac{3}{4},2})$ | D. | $({\frac{1}{2},2})$ |
17.已知函数$f(x)=2sin({ωx+φ})({ω>0,-\frac{π}{2}<φ<\frac{π}{2}})$的部分图象如图所示,则下列结论错误的是( )
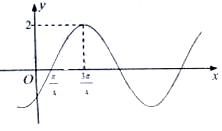

| A. | $φ=-\frac{π}{4}$ | |
| B. | 函数f(x)在$[{-\frac{π}{4},\frac{3π}{4}}]$上单调递增 | |
| C. | 函数f(x)的一条对称轴是$x=\frac{3π}{4}$ | |
| D. | 为了得到函数f(x)的图象,只需将函数y=2cosx的图象向右平移$\frac{π}{4}$个单位 |
4.经过点A(1,2)并且在两个坐标轴上的截距的绝对值相等的直线方程为( )
| A. | y=2x或x-y+1=0 | B. | y=2x,x+y-3=0 | ||
| C. | x+y-3=0,或x-y+1=0 | D. | y=2x,或x+y-3=0,或x-y+1=0 |
1.已知f(x)=$\frac{lnx}{x}$,若f′(x0)=0,则x0=( )
| A. | e2 | B. | e | C. | 1 | D. | ln2 |