题目内容

1．已知f（x）=$\frac{lnx}{x}$，若f′（x0）=0，则x0=（　　）
A．e2B．eC．1D．ln2

分析 根据导数的运算法则求导，再代值计算即可．

解答 解：f（x）的定义域为（0，+∞），
∴f′（x）=（$\frac{lnx}{x}$）′=$\frac{1-lnx}{{x}^{2}}$
由f′（x0）=0，得$\frac{1-lnx}{{x}^{2}}$=0，解得x0=e．
故选：B

点评 本题考查了导数的求导法则，属于基础题．

练习册系列答案
相关题目
11．已知$\frac{π}{2}$＜α＜π，0＜β＜$\frac{π}{2}$，tanα=-$\frac{3}{4}$，cos（β-α）=$\frac{5}{13}$，则sinβ的值为$\frac{63}{65}$．
12．已知函数y=f（x）（x∈I），对函数y=g（x）（x∈I），定义g（x）关于f（x）的“对称函数”为函数y=h（x），x∈I．即y=h（x），x∈I满足对任意x∈I，两点（x，h（x）），（x，g（x））关于点（x，f（x））对称．若h（x）是$g（x）=\sqrt{4-{x^2}}$关于f（x）=3x+m的对称函数，且h（x）＞g（x）恒成立，则实数m的取值范围是（2$\sqrt{10}$，+∞）．
9．函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，则f（x）的解析式是（　　）
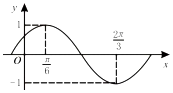
A．$f（x）=sin（x+\frac{π}{6}）$B．$f（x）=sin（x+\frac{π}{3}）$C．$f（x）=sin（2x+\frac{π}{6}）$D．$f（x）=sin（2x+\frac{π}{3}）$
16．一个水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为2的正方形，如图所示，则原平面图形的面积为（　　）
A．4$\sqrt{3}$B．8C．8$\sqrt{3}$D．8$\sqrt{2}$
6．已知$\vec a=（2cosx，\sqrt{3}cosx）$，$\vec b=（cosx，2sinx）$，函数f（x）=$\overrightarrow{a}$•$\overrightarrow{b}$（x∈R）
（1）求函数f（x）的周期；
（2）若方程f（x）-t=1在$x∈[0，\frac{π}{2}]$内恒有两个不相等的实数解，求实数t的取值范围．
13．设函数的定义域为D，若满足条件：存在[a，b]⊆D，使f（x）在[a，b]上的值域为$[{\frac{a}{2}，\frac{b}{2}}]$，则称f（x）为“倍缩函数”．若函数f（x）=ex+t为“倍缩函数”，则实数t的取值范围是（　　）
A．$（{-∞，-\frac{1+ln2}{2}}]$B．$（{-∞，-\frac{1+ln2}{2}}）$C．$[{\frac{1+ln2}{2}，+∞}）$D．$（{\frac{1+ln2}{2}，+∞}）$
10．E、F分别是边长为1的正方形ABCD两对边AD，BC的中点，沿EF把CDEF折起，折成一个二面角D-EF-B是45°的几何图形，下面命题中：
①∠AED=45°；
②异面直线EF与AC所成角的正切值是$\frac{{\sqrt{2-\sqrt{2}}}}{2}$；
③三棱锥C-ABF的体积等于$\frac{{\sqrt{2}}}{48}$．
正确命题的序号有：①②③．
11．函数f（x）=axn（2-x）2在区间[0，2]上的图象如图所示，则n的值可能是（　　）
A．-1B．1C．2D．3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网