题目内容
3.已知f(x)是定义域为(0,+∞)的单调函数,若对任意的x∈(0,+∞),都有$f[{f(x)+{{log}_{\frac{1}{3}}}x}]=4$,且方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解,则实数a的取值范围是( )| A. | 0<a≤5 | B. | a<5 | C. | 0<a<5 | D. | a≥5 |
分析 由题设知必存在唯一的正实数a,满足f(x)+log${\;}_{\frac{1}{3}}$x=a,f(a)=4,f(a)+log${\;}_{\frac{1}{3}}$a=a,故4+log ${\;}_{\frac{1}{3}}$a=a,log${\;}_{\frac{1}{3}}$a=a-4,a=($\frac{1}{3}$)a-4,左增,右减,有唯一解a=3,故f(x)+log ${\;}_{\frac{1}{3}}$x=a=3,由题意可得|log${\;}_{\frac{1}{3}}$x|=x3-6x2+9x-4+a在区间(0,3]上有两解,讨论g(x)=x3-6x2+9x-4+a的单调性和最值,分别画出作出y=|log${\;}_{\frac{1}{3}}$x|,和y=x3-6x2+9x-4的图象,通过平移即可得到a的范围.
解答 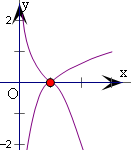 解:∵定义域为(0,+∞)的单调函数f(x)
解:∵定义域为(0,+∞)的单调函数f(x)
满足f[f(x)+log${\;}_{\frac{1}{3}}$x]=4,
∴必存在唯一的正实数a,
满足f(x)+log${\;}_{\frac{1}{3}}$x=a,f(a)=4,①
∴f(a)+log${\;}_{\frac{1}{3}}$a=a,②
由①②得:4+log${\;}_{\frac{1}{3}}$a=a,log${\;}_{\frac{1}{3}}$a=a-4,
a=($\frac{1}{3}$)a-4,左增,右减,有唯一解a=3,
故f(x)+log${\;}_{\frac{1}{3}}$x=a=3,
f(x)=3-log${\;}_{\frac{1}{3}}$x,
由方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解,
即有|log${\;}_{\frac{1}{3}}$x|=x3-6x2+9x-4+a,
由g(x)=x3-6x2+9x-4+a,g′(x)=3x2-12x+9=3(x-1)(x-3),
当1<x<3时,g′(x)<0,g(x)递减;当0<x<1时,g′(x)<0,g(x)递增.
g(x)在x=1处取得最大值a,g(0)=a-4,g(3)=a-4,
分别作出y=|log${\;}_{\frac{1}{3}}$x|,和y=x3-6x2+9x-4的图象,可得
两图象只有一个交点,将y=x3-6x2+9x-4的图象向上平移,
至经过点(3,1),有两个交点,
由g(3)=1即a-4=1,解得a=5,
当0<a≤5时,两图象有两个交点,
即方程|f(x)-3|=x3-6x2+9x-4+a在区间(0,3]上有两解.
故选:A.
点评 本题考查对数的运算性质的综合运用,综合性强,难度大.解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
(2)试估计产量为10吨时,相应的生产能耗.
参考公式:$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$,$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$.
| A. | 15-6$\sqrt{3}$km | B. | 15+6$\sqrt{3}$km | C. | $\sqrt{15+6\sqrt{3}}$km | D. | $\sqrt{15-6\sqrt{3}}$km |
| 经济状况好 | 经济状况一般 | 合计 | |
| 愿意生二胎 | 50 | 50 | 100 |
| 不愿意生二胎 | 20 | 90 | 110 |
| 合计 | 70 | 140 | 210 |
(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?
(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | $({-∞,-\frac{1+ln2}{2}}]$ | B. | $({-∞,-\frac{1+ln2}{2}})$ | C. | $[{\frac{1+ln2}{2},+∞})$ | D. | $({\frac{1+ln2}{2},+∞})$ |