题目内容
4．经过点A（1，2）并且在两个坐标轴上的截距的绝对值相等的直线方程为（ ）| A． | y=2x或x-y+1=0 | B． | y=2x，x+y-3=0 | ||
| C． | x+y-3=0，或x-y+1=0 | D． | y=2x，或x+y-3=0，或x-y+1=0 |
分析 直线在两个坐标轴上的截距的绝对值相等，有三种情况，一是过原点，二是斜率为1，三是斜率为-1，分别求解即可．
解答 解：经过点A（1，2）并且在两个坐标轴上的截距的绝对值相等的直线：
当截距为0时，直线过原点：y=2x；
当斜率为1时，直线方程：x-y+1=0；
当斜率为-1时，直线方程：x+y-3=0．
综上所述，直线方程为y=2x或x+y-3=0或x-y+1=0．
故选D．
点评 本题考查直线的截距和斜率的关系，直线的点斜式方程，是基础题．
练习册系列答案
相关题目
15．国家实行二孩生育政策后，为研究家庭经济状况对生二胎的影响，某机构在本地区符合二孩生育政策的家庭中，随机抽样进行了调查，得到如下的列联表：
（1）请完成上面的列联表，并判断能否在犯错误的概率不超过1%的前提下认为家庭经济状况与生育二胎有关？
（2）若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭，则经济状况好和经济状况一般的家庭分别应抽取多少个？
（3）在（2）的条件下，从中随机抽取2个家庭，求2个家庭都是经济状况好的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| 经济状况好 | 经济状况一般 | 合计 | |
| 愿意生二胎 | 50 | 50 | 100 |
| 不愿意生二胎 | 20 | 90 | 110 |
| 合计 | 70 | 140 | 210 |
（2）若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭，则经济状况好和经济状况一般的家庭分别应抽取多少个？
（3）在（2）的条件下，从中随机抽取2个家庭，求2个家庭都是经济状况好的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
9．函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，则f（x）的解析式是（ ）
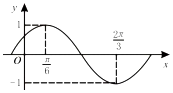
| A． | $f（x）=sin（x+\frac{π}{6}）$ | B． | $f（x）=sin（x+\frac{π}{3}）$ | C． | $f（x）=sin（2x+\frac{π}{6}）$ | D． | $f（x）=sin（2x+\frac{π}{3}）$ |
16．
一个水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为2的正方形，如图所示，则原平面图形的面积为（ ）
一个水平放置的平面图形，用斜二测画法画出了它的直观图，此直观图恰好是一个边长为2的正方形，如图所示，则原平面图形的面积为（ ）| A． | 4$\sqrt{3}$ | B． | 8 | C． | 8$\sqrt{3}$ | D． | 8$\sqrt{2}$ |
13．设函数的定义域为D，若满足条件：存在[a，b]⊆D，使f（x）在[a，b]上的值域为$[{\frac{a}{2}，\frac{b}{2}}]$，则称f（x）为“倍缩函数”．若函数f（x）=ex+t为“倍缩函数”，则实数t的取值范围是（ ）
| A． | $（{-∞，-\frac{1+ln2}{2}}]$ | B． | $（{-∞，-\frac{1+ln2}{2}}）$ | C． | $[{\frac{1+ln2}{2}，+∞}）$ | D． | $（{\frac{1+ln2}{2}，+∞}）$ |
14．下列函数中，与函数$f（x）=\frac{1}{{\root{3}{x}}}$的定义域相同的函数是（ ）
| A． | y（x）=x•ex | B． | $y=\frac{sinx}{x}$ | C． | $y=\frac{x}{sinx}$ | D． | $y=\frac{lnx}{x}$ |