题目内容
20．已知$f（x）=\left\{\begin{array}{l}x+1，（{0≤x＜1}）\\{2^x}-\frac{1}{2}，（{x≥1}）\end{array}\right.$，设a＞b≥0，若f（a）=f（b），则b•f（a）的取值范围是（ ）| A． | （1，2] | B． | $（{\frac{3}{4}，2}]$ | C． | $[{\frac{3}{4}，2}）$ | D． | $（{\frac{1}{2}，2}）$ |
分析 作函数$f（x）=\left\{\begin{array}{l}x+1，（{0≤x＜1}）\\{2^x}-\frac{1}{2}，（{x≥1}）\end{array}\right.$的图象，从而利用数形结合知2-$\frac{1}{2}$≤b+1＜2，可得b的范围，由f（a）=1+b，求得范围，由不等式的性质从而解得所求范围．
解答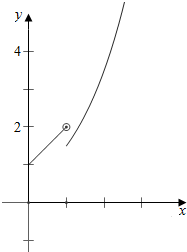 
解：作函数$f（x）=\left\{\begin{array}{l}x+1，（{0≤x＜1}）\\{2^x}-\frac{1}{2}，（{x≥1}）\end{array}\right.$的图象如下，
结合图象可知，
2-$\frac{1}{2}$≤b+1＜2，
解得$\frac{1}{2}$≤b＜1，
f（a）=f（b）=1+b，
由$\frac{3}{2}$≤f（a）＜2，
可得$\frac{3}{4}$≤b•f（a）＜2，
故选：C．
点评 本题考查了数形结合的思想应用及方程的根与函数的图象的交点的关系应用，属于中档题．
练习册系列答案
相关题目
15．国家实行二孩生育政策后，为研究家庭经济状况对生二胎的影响，某机构在本地区符合二孩生育政策的家庭中，随机抽样进行了调查，得到如下的列联表：
（1）请完成上面的列联表，并判断能否在犯错误的概率不超过1%的前提下认为家庭经济状况与生育二胎有关？
（2）若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭，则经济状况好和经济状况一般的家庭分别应抽取多少个？
（3）在（2）的条件下，从中随机抽取2个家庭，求2个家庭都是经济状况好的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| 经济状况好 | 经济状况一般 | 合计 | |
| 愿意生二胎 | 50 | 50 | 100 |
| 不愿意生二胎 | 20 | 90 | 110 |
| 合计 | 70 | 140 | 210 |
（2）若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭，则经济状况好和经济状况一般的家庭分别应抽取多少个？
（3）在（2）的条件下，从中随机抽取2个家庭，求2个家庭都是经济状况好的概率．
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
5．直线3x+4y+a=0上存在点M满足过点M作圆（x-2）2+（y-1）2=2的两条切线互相垂直，则a的取值范围是（ ）
| A． | （-20，0] | B． | [-20，0] | C． | [-20，0） | D． | （-20，0） |
9．函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的部分图象如图所示，则f（x）的解析式是（ ）
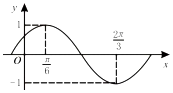
| A． | $f（x）=sin（x+\frac{π}{6}）$ | B． | $f（x）=sin（x+\frac{π}{3}）$ | C． | $f（x）=sin（2x+\frac{π}{6}）$ | D． | $f（x）=sin（2x+\frac{π}{3}）$ |