题目内容
若命题“?x∈R，使得x2-a≤0成立”为假命题，则实数a的取值范围为 ．
考点：特称命题,命题的真假判断与应用
专题：计算题,简易逻辑
分析：将原命题转化为命题的否定为真，从而运用二次不等式的恒成立解决，本题只要由判别式小于0，解出即可．
解答：
解：命题“?x∈R，使得x2-a≤0成立”为假命题，
则命题的否定“?x∈R，x2-a＞0恒成立”为真命题．
由判别式小于0得，0+4a＜0，解得，a＜0．
故实数a的取值范围为（-∞，0）．
故答案为：（-∞，0）．
则命题的否定“?x∈R，x2-a＞0恒成立”为真命题．
由判别式小于0得，0+4a＜0，解得，a＜0．
故实数a的取值范围为（-∞，0）．
故答案为：（-∞，0）．
点评：本题考查存在性命题的真假，考查可以运用命题的否定为真，转化为二次不等式恒成立问题，属于基础题．
练习册系列答案
快捷英语周周练系列答案
相关题目
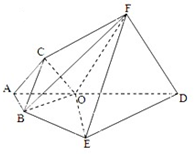如图，ABEDFC为多面体，平面ABED与平面ACFD垂直，点O在线段AD上，OA=1，OD=2，△OAB，△OAC，△ODF，△ODE都是正三角形．