题目内容
设函数f(x)=
(x>0),定义f1(x)=f(x)=
,当n∈N+且n≥2时,fn+1(x)=f[fn(x)](n为正整数),则f3(x)= ;fn(x)= .
| x |
| x+2 |
| x |
| x+2 |
考点:函数的值
专题:函数的性质及应用
分析:分别计算出f1(x),f2(x),f3(x),…,分析不等式的构成,寻找规律,进行归纳.
解答:
解:∵函数f1(x)=f(x)=
(x>0),n≥2时,fn+1(x)=f[fn(x)](n为正整数),
∴f2(x)=f(f1(x))=
=
,
f3(x)=f(f2(x))=
=
,
同理可得f4(x)=f(f3(x))=
…
所给的函数式的分子不变都是x,
而分母是由两部分的和组成,
第一部分的系数分别是1,3,7,15…2n-1,
第二部分的数分别是2,4,8,16…2n
∴fn(x)=f(fn-1(x))=
,
故答案为:
,
.
| x |
| x+2 |
∴f2(x)=f(f1(x))=
| ||
|
| x |
| 3x+4 |
f3(x)=f(f2(x))=
| ||
|
| x |
| 7x+8 |
同理可得f4(x)=f(f3(x))=
| x |
| 15x+16 |
…
所给的函数式的分子不变都是x,
而分母是由两部分的和组成,
第一部分的系数分别是1,3,7,15…2n-1,
第二部分的数分别是2,4,8,16…2n
∴fn(x)=f(fn-1(x))=
| x |
| (2n-1)x+2n |
故答案为:
| x |
| 7x+8 |
| x |
| (2n-1)x+2n |
点评:本题考查归纳推理,实际上可看作给出一个数列的前几项写出数列的通项公式.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
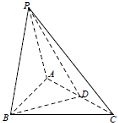 如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.
如图,在三棱锥P-ABC中,PA=PB=AB=BC,∠PBC=90°,D为AC的中点,AB⊥PD.