题目内容
△ABC中,已知A(-1,2),B(3,4),C(-2,5).
(1)求BC边上的高AH所在的直线方程;
(2)求△ABC的面积.
(1)求BC边上的高AH所在的直线方程;
(2)求△ABC的面积.
考点:直线的一般式方程与直线的垂直关系,点到直线的距离公式
专题:直线与圆
分析:(1)求出kBC=-
,得kAH=5,由此能求出AH所在的直线方程.
(2)求出BC所在的直线方程为x+5y-23=0.求出点A到直线BC的距离d=
,再求出|BC|,由此能求出S△ABC.
| 1 |
| 5 |
(2)求出BC所在的直线方程为x+5y-23=0.求出点A到直线BC的距离d=
7
| ||
| 13 |
解答:
解:(1)∵△ABC中,A(-1,2),B(3,4),C(-2,5),
∴kBC=
=-
,∴kAH=5,…(2分)
∴AH所在的直线方程为y-2=5(x+1),
整理,得5x-y+7=0.…(4分)
(2)BC所在的直线方程为y-4=-
(x-3),
即x+5y-23=0.…(5分)
点A到直线BC的距离为d=
=
,…(7分)
又|BC|=
=
,…(9分)
∴S△ABC=
×|BC|×d=
×
=7.…(10分)
∴kBC=
| 4-5 |
| 3-(-2) |
| 1 |
| 5 |
∴AH所在的直线方程为y-2=5(x+1),
整理,得5x-y+7=0.…(4分)
(2)BC所在的直线方程为y-4=-
| 1 |
| 5 |
即x+5y-23=0.…(5分)
点A到直线BC的距离为d=
| |-1+10-23| | ||
|
7
| ||
| 13 |
又|BC|=
| (3+2)2+(4-5)2 |
| 26 |
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
| 26 |
7
| ||
| 13 |
点评:本题考查直线方程的求法,考查三角形面积的求法,解题时要认真审题,注意点到直线的距离公式的合理运用.

练习册系列答案
相关题目
 如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.
如图,已知⊙O的直径AB=3,点C为⊙O上异于A,B的一点,VC⊥平面ABC,且VC=2,点M为线段VB的中点.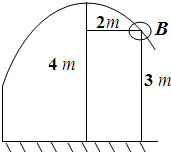 有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?
有一次姚明投篮时,测得投篮的轨迹是抛物线,如图所示,抛物线最高点离地面距离4m,篮筐B高为3m,篮筐中心离最高点的水平距离为2m,求投中时抛物线的方程?