题目内容
已知函数f(x)对任意的实数x、y都有f(x+y)=f(x)+f(y)-1,且当x>0时,f(x)>1.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式f(x2-ax+5a)<f(m)的解集为{x|-3<x<2},求m的值.
(3)若f(1)=2,求f(2013)的值.
(1)求证:函数f(x)在R上是增函数;
(2)若关于x的不等式f(x2-ax+5a)<f(m)的解集为{x|-3<x<2},求m的值.
(3)若f(1)=2,求f(2013)的值.
考点:抽象函数及其应用,函数单调性的性质
专题:函数的性质及应用
分析:(1)利用定义证明单调性,要能够很好的利用f(x+y)=f(x)+f(y)-1,且当x>0时,f(x)>1这两个条件,
(2)根据原函数的单调性可得对应的一元二次不等式,由于其解集已经知道,于是得到方程x2-ax+5a-m=0的根为-3和2,利用根与系数的关系可以求出.
(3)通过赋值法可得到f(n)-f(n-1)=1,累加可得.
(2)根据原函数的单调性可得对应的一元二次不等式,由于其解集已经知道,于是得到方程x2-ax+5a-m=0的根为-3和2,利用根与系数的关系可以求出.
(3)通过赋值法可得到f(n)-f(n-1)=1,累加可得.
解答:
解:(1)设x1,x2,x1-x2>0,
∵当x>0时,f(x)>1.
∴f(x1-x2)>1,
∴f(x1)=f(x1-x2+x2)=f(x1-x2)+f(x2)-1
∴f(x1)-f(x2)=f(x1-x2)-1>0,
故函数f(x)在R上是增函数;
(2)由(1)知函数f(x)在R上是增函数;
∵不等式f(x2-ax+5a)<f(m),
∴x2-ax+5a<m,
即x2-ax+5a-m<0,
∵关于x的不等式f(x2-ax+5a)<f(m)的解集为{x|-3<x<2},
∴方程x2-ax+5a-m=0的根为-3和2,
∴-3+2=a,-3×2=5a-m,
解得a=-1,m=1,
(3)∵f(1)=2
令x=n-1,y=1,得f(n)-f(n-1)=1,
令x=n-2,y=1,得f(n-1)-f(n-2)=1
…
令x=1,y=1得f(2)-f(1)=1,
所以累加可得,f(n)=2+(n-1)×1=n+1,
故f(2013)=2014.
∵当x>0时,f(x)>1.
∴f(x1-x2)>1,
∴f(x1)=f(x1-x2+x2)=f(x1-x2)+f(x2)-1
∴f(x1)-f(x2)=f(x1-x2)-1>0,
故函数f(x)在R上是增函数;
(2)由(1)知函数f(x)在R上是增函数;
∵不等式f(x2-ax+5a)<f(m),
∴x2-ax+5a<m,
即x2-ax+5a-m<0,
∵关于x的不等式f(x2-ax+5a)<f(m)的解集为{x|-3<x<2},
∴方程x2-ax+5a-m=0的根为-3和2,
∴-3+2=a,-3×2=5a-m,
解得a=-1,m=1,
(3)∵f(1)=2
令x=n-1,y=1,得f(n)-f(n-1)=1,
令x=n-2,y=1,得f(n-1)-f(n-2)=1
…
令x=1,y=1得f(2)-f(1)=1,
所以累加可得,f(n)=2+(n-1)×1=n+1,
故f(2013)=2014.
点评:本题主要考查了利用赋值法求解函数的函数值,判断函数的奇偶性、单调性及利用单调性求解不等式等函数知识的综合应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
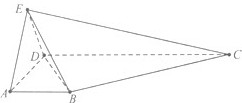 如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC=
如图所示,在四棱锥E-ABCD中,AB∥CD,∠ADC=90°,CD=3,AB=1,EA=AD=DE=2,EC= 如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证:
如图,直三棱柱ABC-A1B1C1中,B1C1=A1C1,AC1⊥A1B,M,N分别是A1B1,AB的中点,求证: