题目内容
设函数f(x)=lnx,g(x)=
(a>0)
(1)当a=2时,求h(x)=f(x)+g(x)的最小值;
(2)若h(x)=f(x)+g(x),在(0,+∞)上有两个不同的零点,求a的取值范围;
(3)证明:
>
-
ln(n!)
| a |
| x |
(1)当a=2时,求h(x)=f(x)+g(x)的最小值;
(2)若h(x)=f(x)+g(x),在(0,+∞)上有两个不同的零点,求a的取值范围;
(3)证明:
| n |
 |
| k=1 |
| 1 |
| k |
| nln(2e) |
| 2 |
| 1 |
| 2 |
考点:利用导数求闭区间上函数的最值
专题:导数的综合应用
分析:(1)将a=2带人,得出h(x),利用求导数判断单调性,从而求出最小值.
(2)判断函数h(x)在(0,+∞)上的单调性,有无最值,要是最大值,根据条件需限制它大于0,若是最小值需限制它小于0,从而求出a的取值范围.
(3)你可以把要证明的不等式展开,只要证明展开后的不等式即可.通过观察展开后的式子,要用上第一问的结论,这一点很关键,用上这个结论,答案很容易解出了.
(2)判断函数h(x)在(0,+∞)上的单调性,有无最值,要是最大值,根据条件需限制它大于0,若是最小值需限制它小于0,从而求出a的取值范围.
(3)你可以把要证明的不等式展开,只要证明展开后的不等式即可.通过观察展开后的式子,要用上第一问的结论,这一点很关键,用上这个结论,答案很容易解出了.
解答:
解:(1)a=2时,h(x)=lnx+
,则h′(x)=
,所以0<x<2时,h′(x)<0;x>2时,h′(x)>0;
所以,h(x)的最小值是h(2)=ln2+1.
(2)h(x)=lnx+
,则h′(x)=
,所以x∈(0,a)时,h′(x)<0;x∈(a,+∞)时,h′(x)>0;
所以,x=a时,h(x)取最小值h(a)=lna+1;
∵h(x)在(0,+∞)有两个不同的零点,∴lna+1<0,∴0<a<
.
(3)要证
>
-
ln(n!);
即证:1+
+
+…+
>
-
(ln1+ln2+ln3+…+lnn)
由(1)知:x>0时,lnx+
≥ln2+1,当且仅当x=2时取“=”.
∴
lnx+
≥
即:
≥
-
lnx;
∴1>
-
ln1
≥
-
ln2
>
-
ln3
…
>
-
lnn
以上各式相加得:
>
ln(n!).
| 2 |
| x |
| x-2 |
| x2 |
所以,h(x)的最小值是h(2)=ln2+1.
(2)h(x)=lnx+
| a |
| x |
| x-a |
| x2 |
所以,x=a时,h(x)取最小值h(a)=lna+1;
∵h(x)在(0,+∞)有两个不同的零点,∴lna+1<0,∴0<a<
| 1 |
| e |
(3)要证
| n |
 |
| k=1 |
| 1 |
| k |
| nln(2e) |
| 2 |
| 1 |
| 2 |
即证:1+
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| n(ln2+1) |
| 2 |
| 1 |
| 2 |
由(1)知:x>0时,lnx+
| 2 |
| x |
∴
| 1 |
| 2 |
| 1 |
| x |
| ln2+1 |
| 2 |
即:
| 1 |
| x |
| ln2+1 |
| 2 |
| 1 |
| 2 |
∴1>
| ln2+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| ln2+1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| ln2+1 |
| 2 |
| 1 |
| 2 |
…
| 1 |
| n |
| ln2+1 |
| 2 |
| 1 |
| 2 |
以上各式相加得:
| n |
 |
| k=1 |
| 1 |
| k |
| 1 |
| 2 |
点评:第一二问都用到了求导数的方法,而第二问求a的取值范围,注意对最值的限制就可以了.最后一问的关键就是用上第一问的结论,这需要你的观察能力.

练习册系列答案
 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
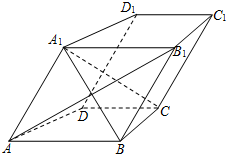 如图,在四棱柱ABCD-A1B1C1D1中,AB1⊥BC,AB∥CD,BC⊥AB且AA1=AB=AD=2,∠A1AB=∠DAB=60°.
如图,在四棱柱ABCD-A1B1C1D1中,AB1⊥BC,AB∥CD,BC⊥AB且AA1=AB=AD=2,∠A1AB=∠DAB=60°.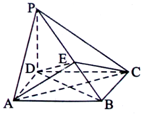 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,四边形ABCD是边长为2的菱形,∠ABC=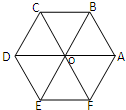 (1)如图,正六边形ABCDEF中,点O为其中心,以这七个点为起点与终点的向量中,与向量
(1)如图,正六边形ABCDEF中,点O为其中心,以这七个点为起点与终点的向量中,与向量