题目内容
已知函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=sin2x,则f(-
)=( )
| 17π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
考点:正弦函数的奇偶性,函数奇偶性的性质,函数的值
专题:函数的性质及应用,三角函数的求值
分析:利用函数的单调性得出f(-
)=f(
)=sin
=(6π-
)=-
,判断求解即可
| 17π |
| 6 |
| 17π |
| 6 |
| 17π |
| 3 |
| π |
| 3 |
| ||
| 2 |
解答:
解:∵函数f(x)是定义在R上的偶函数,当x≥0时,f(x)=sin2x,
∴f(-
)=f(
)=sin
=(6π-
)=-
故选:D
∴f(-
| 17π |
| 6 |
| 17π |
| 6 |
| 17π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故选:D
点评:本题综合考察了函数的奇偶性,三角函数的运用求解,属于中档题.

练习册系列答案
相关题目
已知一个算法的流程图如图所示,则输出的结果是( )
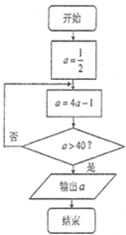

| A、3 | B、11 | C、43 | D、171 |
在△ABC中,A,B,C所对的边长分别是a,b,c且A=30°,B=45°,a=3,则b=( )
A、
| ||
B、2
| ||
C、3
| ||
D、4
|
已知f(x)=x2(1nx-a)+a,则下列结论中错误的是( )
| A、?a>0,?x>0,f(x)≥0 |
| B、?a>0,?x>0,f(x)≤0 |
| C、?a>0,?x>0,f(x)≥0 |
| D、?a>0,?x>0,f(x)≤0 |