题目内容
2.已知幂函数f(x)的图象经过点$(\frac{1}{2},4)$,则$f(\sqrt{2})$=$\frac{1}{2}$.分析 用待定系数法求出幂函数y=f(x)的解析式,再计算$f(\sqrt{2})$的值.
解答 解:设幂函数y=f(x)=xα,α∈R
其图象过点$(\frac{1}{2},4)$,
所以${(\frac{1}{2})}^{α}$=4,
解得α=-2,
所以f(x)=x-2;
所以$f(\sqrt{2})$=${(\sqrt{2})}^{-2}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了用待定系数法求函数解析式的应用问题,是基础题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
10.将函数y=(2x-2)ex-1的图象向左平移1个单位得到函数f(x)的图象,则( )
| A. | x=-$\frac{1}{2}$为f(x)的极大值点 | B. | x=1为f(x)的极小值点 | ||
| C. | x=-1为f(x)的极大值点 | D. | x=-1为f(x)的极小值点 |
17.若直线2ax-by+2=0 (a>0,b>0)恰过(-1,1),则$\frac{1}{a}+\frac{2}{b}$的最小值为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
7.在如图所示的程序框图中,若a=($\frac{1}{16}$)${\;}^{\frac{1}{2}}$,b=log42,c=log23•log32,则输出的x等于( )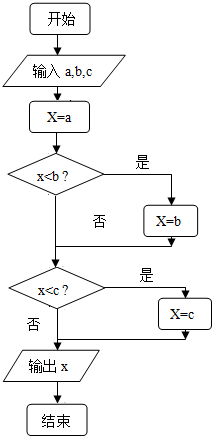

| A. | 0.25 | B. | 0.5 | C. | 1 | D. | 2 |
14.已知一个算法的程序框图如图所示,当输出的结果为0时,输入的x的值为( )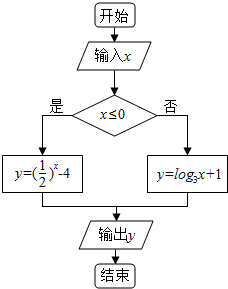

| A. | -2 | B. | -2或-1 | C. | 1或-3 | D. | -2或$\frac{1}{3}$ |
12.下列说法错误的是( )
| A. | 若命题“p∧q”为真命题,则“p∨q”为真命题 | |
| B. | 命题“若m>0,则方程x2+x-m=0有实根”的逆命题为真命题 | |
| C. | 命题“若a>b,则ac2>bc2”的否命题为真命题 | |
| D. | 若命题“¬p∨q”为假命题,则“p∧¬q”为真命题 |
