题目内容
13.下列说法中,正确的有( )①若任意x1,x2∈A,当x1<x2时,$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}$>0,则y=f(x)在A上是增函数;
②函数y=x2在R上是增函数;
③函数y=-$\frac{1}{x}$在定义域上是增函数;
④函数y=$\frac{1}{x}$的单调区间是(-∞,0)∪(0,+∞).
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据增函数的定义便可判断①正确,而根据二次函数和反比例函数在定义域上没有单调性便可判断出②③④不正确,从而可找到正确选项.
解答 解:①∵x1<x2,
∴由$\frac{f({x}_{1})-f({x}_{2})}{{x}_{1}-{x}_{2}}>0$得,f(x1)<f(x2);
∴由增函数的定义知该说法正确;
②y=x2在R上没有单调性,∴该说法错误;
③反比例函数$y=-\frac{1}{x}$在定义域上没有单调性,∴该说法错误;
④y=$\frac{1}{x}$在定义域上没有单调性,∴(-∞,0)∪(0,+∞)不是该函数的单调区间,∴该说法错误;
∴说法正确的个数为1.
故选:B.
点评 考查增函数的定义,以及二次函数、反比例函数在定义域上的单调性.

练习册系列答案
相关题目
1.若变量x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{y≥0}\\{3x+4y≤12}\end{array}\right.$则z=x-y的最大值为( )
| A. | 8 | B. | 16 | C. | 3 | D. | 4 |
3.已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:小时)的函数,记作:y=f(t),下表是某日各时的浪高数据:
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b(A>0,ω>0)
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式
(2)依据规定,当海浪高度高于0.75米时才对冲浪爱好者开放,则一天内的上午8:00至晚上24:00之间,有多少时间可供冲浪爱好者进行运动?
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.5 | 1.0 | 0.5 | 1.0 | 1.5 | 1 | 0.5 | 0.99 | 1.5 |
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式
(2)依据规定,当海浪高度高于0.75米时才对冲浪爱好者开放,则一天内的上午8:00至晚上24:00之间,有多少时间可供冲浪爱好者进行运动?
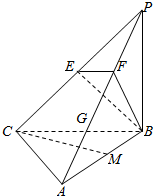 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=4,E为PC的中点,M为AB的中点,点G,F是PA上的三等分点.