题目内容
(1)设点A(p,q)在|p|≤3,|q|≤3范围内均匀分布,求一元二次方程x2-2px-q2+1=0有实根的概率.
(2)p是从0,1,2,3四个数中任取的一个数,q是从0,1,2,三个数中任取的一个数,求上述x2-2px-q2+1=0有实根的概率.
(2)p是从0,1,2,3四个数中任取的一个数,q是从0,1,2,三个数中任取的一个数,求上述x2-2px-q2+1=0有实根的概率.
考点:几何概型,古典概型及其概率计算公式
专题:计算题
分析:(1)求方程x2-2px-q2+1=0有实数根的概率,先根据二次方程根的判别式求出p,q必须满足的条件,再在坐标系中画出相应的封闭曲线,最后求出它们的面积比即可.
(2)根据一元二次方程根的存在情况可得△≥0,方程有解,列举出6种等可能的结果,其中只有p=0,q=1使△<0,即使△≥0有5种情况,最后根据概率的概念求解即可;
(2)根据一元二次方程根的存在情况可得△≥0,方程有解,列举出6种等可能的结果,其中只有p=0,q=1使△<0,即使△≥0有5种情况,最后根据概率的概念求解即可;
解答:
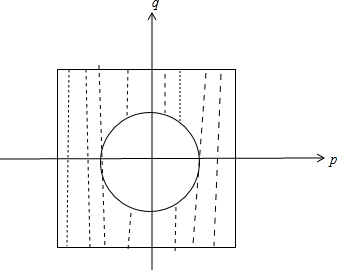 (1)解:由|p|≤3,|q|≤3可知(p,q)边长为6的正方形区域的点集构成
(1)解:由|p|≤3,|q|≤3可知(p,q)边长为6的正方形区域的点集构成
方程均为实数根的条件是:判别式△=4p2-4(-q2+1)≥0
即p2+q2≥1
在直接坐标系点(p,q)落在以原点为圆心,以1为半径的圆上或其外部
单位圆面积为π,正方形面积为6×6=36
则概率为
=1-
π
(2)由题意可得,本题是一个古典概率
设事件A:“方程x2-2px-q2+1=0有实数根”
当P>0,q>0时,x2-2px-q2+1=0有实数根的充要条件为p≥q
基本事件共有(0,0),(0,1),(0,2),(1,0),1,1)(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)
事件A包含9个基本事件
事件A的概率P(A)=
=
 (1)解:由|p|≤3,|q|≤3可知(p,q)边长为6的正方形区域的点集构成
(1)解:由|p|≤3,|q|≤3可知(p,q)边长为6的正方形区域的点集构成方程均为实数根的条件是:判别式△=4p2-4(-q2+1)≥0
即p2+q2≥1
在直接坐标系点(p,q)落在以原点为圆心,以1为半径的圆上或其外部
单位圆面积为π,正方形面积为6×6=36
则概率为
| 36-π |
| 36 |
| 1 |
| 36 |
(2)由题意可得,本题是一个古典概率
设事件A:“方程x2-2px-q2+1=0有实数根”
当P>0,q>0时,x2-2px-q2+1=0有实数根的充要条件为p≥q
基本事件共有(0,0),(0,1),(0,2),(1,0),1,1)(1,2),(2,0),(2,1),(2,2),(3,0),(3,1),(3,2)
事件A包含9个基本事件
事件A的概率P(A)=
| 9 |
| 12 |
| 3 |
| 4 |
点评:本题主要考查了几何概型,古典概率的求解公式的应用,要注意两者之间的联系与区别

练习册系列答案
相关题目
已知直线ax+by+c=0,(a,b,c≠0)与圆x2+y2=1相切,则以|a|,|b|,|c|为边( )
| A、不能组成三角形 |
| B、组成锐角三角形 |
| C、组成直角三角形 |
| D、组成钝角三角形 |
若x2+y2+(λ-1)x+2λy+λ=0表示圆,则λ的取值范围是( )
| A、λ>0 | ||
B、
| ||
C、λ>1或λ<
| ||
| D、λ∈R |
设集合A={x|
<0},B={y|y=2x,x>0},则A∩B=( )
| x |
| x-2 |
| A、(0,2) |
| B、(1,2) |
| C、(0,1) |
| D、(一∞,0) |