题目内容
函数f(x)=3sin(2x-
)+5的相邻两条对称轴间的距离为 .
| π |
| 4 |
考点:函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:求出函数的周期,然后求出函数y=2sin(2x-
)的图象的两条相邻对称轴间的距离.
| π |
| 4 |
解答:
解:函数y=2sin(2x-
)的周期是:T=
=π,图象的两条相邻对称轴间的距离就是最大值与最小值时的x的差值为
,
故答案为:
.
| π |
| 4 |
| 2π |
| 2 |
| π |
| 2 |
故答案为:
| π |
| 2 |
点评:本题是基础题,考查三角函数的周期的应用,图象的两条相邻对称轴间的距离就是最大值与最小值的距离的差值是解题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
正项等比数列{an}满足:a3=a2+2a1,若存在am,an,使得aman=16a12,则
+
的最小值为( )
| 1 |
| m |
| 4 |
| n |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知双曲线的焦距为2
,离心率
,则双曲线的标准方程是( )
| 3 |
| 3 |
A、x2-
| ||||||||
B、
| ||||||||
C、x2-
| ||||||||
D、
|
执行如图所示的程序框图,输出的S值为( )


| A、9 | B、19 | C、20 | D、35 |
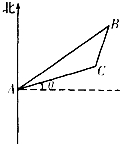 如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20
如图所示,位于东海某岛的雷达观测站A,发现其北偏东45°,与观测站A距离20