题目内容
11.已知函数f(x)=$\frac{2a}{e}$x-lnx(a∈R,e为自然对数的底数).(Ⅰ)讨论函数f(x)的极值点;
(Ⅱ)当a=1时,求证:f(x)-$\frac{{x}^{2}}{{e}^{x}}$>0.
分析 (Ⅰ)求出函数的导数,通过讨论a的范围,确定函数的单调性,判断函数的极值点即可;
(Ⅱ)令g(x)=$\frac{{x}^{2}}{{e}^{x}}$,问题转化为证明f(x)min>g(x)max,根据函数的单调性,分别求出其最小值和最大值,从而证出结论.
解答 解:(Ⅰ)f(x)的定义域是(0,+∞),
f′(x)=$\frac{2a}{e}$-$\frac{1}{x}$,
a≤0时,f′(x)<0,f(x)递减,无极值;
a>0时,令f′(x)>0,解得:x>$\frac{e}{2a}$,
令f′(x)<0,解得:x<$\frac{e}{2a}$,
∴f(x)在(0,$\frac{e}{2a}$)递减,在($\frac{e}{2a}$,+∞)递增,
∴x=$\frac{e}{2a}$是函数的极小值点;
(Ⅱ)证明:a=1时,f(x)=$\frac{2}{e}$x-lnx,
由(Ⅰ)f(x)的最小值是f($\frac{e}{2}$)=ln2≈0.693,
令g(x)=$\frac{{x}^{2}}{{e}^{x}}$,(x>0),g′(x)=$\frac{x(2-x)}{{e}^{x}}$,
令g′(x)>0,解得:0<x<2,令g′(x)<0,解得:x>2,
∴g(x)在(0,2)递增,在(2,+∞)递减,
∴g(x)max=g(2)=$\frac{4}{{e}^{2}}$≈0.545,
故f(x)min>g(x)max,
故当a=1时,f(x)-$\frac{{x}^{2}}{{e}^{x}}$>0.
点评 本题考查了函数的单调性、极值、最值问题,考查导数的应用,是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知向量|$\overrightarrow a}$|=4,$\overrightarrow e$为单位向量,当他们之间的夹角为$\frac{π}{3}$时,$\overrightarrow{a}$在$\overrightarrow{e}$方向上的投影与$\overrightarrow{e}$在$\overrightarrow{a}$方向上的投影分别为( )
| A. | 2$\sqrt{3}$,$\frac{\sqrt{3}}{2}$ | B. | 2,$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$,2$\sqrt{3}$ | D. | 2,2 |
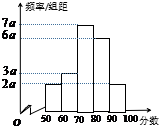 在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).
在一次数学测试中,某班40名学生的成绩频率分布直方图如图所示(学生成绩都在[50,100]之间).