题目内容
6.根据已知向量$\overrightarrow{a}$、$\overrightarrow{b}$,求作$\overrightarrow{a}$+$\overrightarrow{b}$、$\overrightarrow{a}$-$\overrightarrow{b}$.(1

(2

(3

分析 利用向量加减运算的三角形法则作图.
解答 解:(1)作出$\overrightarrow{a}+\overrightarrow{b}$,如图所示: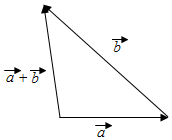
作出$\overrightarrow{a}-\overrightarrow{b}$如图所示: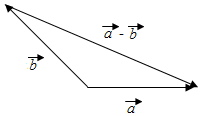
(2)作出$\overrightarrow{a}+\overrightarrow{b}$,如图所示: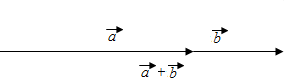
作出$\overrightarrow{a}-\overrightarrow{b}$如图所示:
(3)作出$\overrightarrow{a}+\overrightarrow{b}$,如图所示: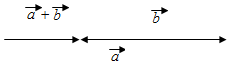
作出$\overrightarrow{a}-\overrightarrow{b}$如图所示: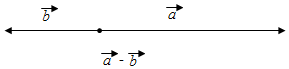
点评 本题考查了平面向量加减运算的几何意义,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.若a+b=5,则a>0,b>0是ab有最大值$\frac{25}{4}$的( )
| A. | 必要非充分条件 | B. | 充要条件 | ||
| C. | 充分非必要条件 | D. | 既非充分也非必要条件 |
17.在以O为中心,F1,F2为焦点的双曲线上存在一点M,满足|$\overrightarrow{M{F}_{1}}$|=2|$\overrightarrow{MO}$|=2|$\overrightarrow{M{F}_{2}}$|,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{6}$ |
3.已知双曲线E的左,右顶点为A,B,点C在E上,AB=BC,且∠BCA=30°,则E的离心率为( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
1.已知双曲线C:$\frac{y^2}{a^2}-\frac{x^2}{b^2}=1$的焦距为$10\sqrt{5}$,点P(1,2)在双曲线C的渐近线上,则双曲线C的方程为( )
| A. | $\frac{y^2}{20}-\frac{x^2}{5}=1$ | B. | $\frac{y^2}{5}-\frac{x^2}{20}=1$ | C. | $\frac{y^2}{100}-\frac{x^2}{25}=1$ | D. | $\frac{y^2}{25}-\frac{x^2}{100}=1$ |
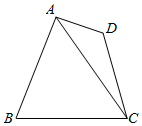 如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.
如图所示,在四边形ABCD中,已知BA⊥AD,AB=10,BC=5$\sqrt{6}$,∠BAC=60°,∠ADC=135°,CD=$\frac{5\sqrt{2}}{2}$.