题目内容

直线
x=1-
2
t
y=2+
2
t
（t为参数）上到点A（1，2）的距离为4
2
的点的坐标为
 
．
考点：参数方程化成普通方程
专题：坐标系和参数方程
分析：由两点间距离公式直接求解即可．
解答： 解：点P（x，y）为直线上的点|PA|=
(1-
2
t-1)2+(2+
2
t-2)2
=4
2
，解得t=2
2
或t=-2
2
，
故P（-3，6）或（5，-2）．
故答案为：（-3，6）或（5，-2）．
点评：本题考查直线的参数方程的应用，两点的距离公式的应用，考查计算能力．
练习册系列答案
相关题目
函数y=sin2x的图象中相邻两条对称轴的距离为
 
．
若a≤b，则ac2≤bc2，则命题的原命题、逆命题、否命题和逆否命题中正确命题的个数是
 
．
已知tan（π+α）=-
1
3
，且α是钝角，又α-β是锐角，sin（α-β）=
3
5
，sinβ=
 
．
将边长为1的正方形ABCD沿对角线BD折成直二面角，若点P满足
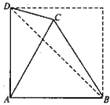
BP
=
1
2
BA
-
1
2
BC
+
BD
，则|
BP
|的值为（　　）
A、
3
2
B、2
C、
10-
2
4
D、
9
4
已知数列{an}满足an=n•sin（
nπ
2
），（n∈N*），则a1+a2+…+a250=
 
．
如果实数x，y满足不等式组
x≥1
x-y+1≥
2x-y-2≤0
0试求：
（1）
y
x
的最大值；
（2）x2+y2的最小值．
函数f（x）=2|x|-1在区间[-1，2]的值域是（　　）
A、[1，4]
B、[
1
2
，2]
C、[1，2]
D、[
1
2
，1]
函数f（x）=x2+2的值域是
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网