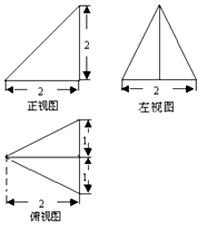
题目内容
16.已知命题p:?x∈R,x2-2xsinθ+1≥0;命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,则下列命题中的真命题为( )| A. | (¬p)∧q | B. | p∧(¬q) | C. | (¬p)∨q | D. | ¬(p∨q) |
分析 分别判断出p,q的真假,从而判断出复合命题的真假即可.
解答 解:关于命题p:?x∈R,x2-2xsinθ+1≥0,△=4sin2θ-4≤0,故p是真命题,
关于命题q:?α,β∈R,sin(α+β)≤sinα+sinβ,是真命题,
∴(¬p)∨q是真命题,
故选:C.
点评 本题考查了复合命题的判断,考查二次函数以及三角函数问题,是一道基础题.

练习册系列答案
相关题目
6.已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$,点A(c,b),右焦点F(c,0),椭圆上存在一点M,使得$\overrightarrow{OM}•\overrightarrow{OA}=\overrightarrow{OF}•\overrightarrow{OA}$,且$\overrightarrow{OM}+\overrightarrow{OF}=t\overrightarrow{OA}({t∈R})$,则该椭圆的离心率为( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{{\sqrt{3}}}{2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{\sqrt{2}}}{3}$ |
4.如图所示,在△ABC中,D为BC的中点,BP丄DA,垂足为P,且BP=2,则$\overrightarrow{BC}$•$\overrightarrow{BP}$=( )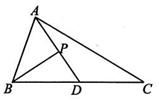

| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
8.若i为虚数单位,则复数$\frac{1+i}{3-i}$等于( )
| A. | $\frac{1}{2}+\frac{1}{2}i$ | B. | $\frac{1}{4}+\frac{1}{2}i$ | C. | $\frac{2}{5}+\frac{2}{5}i$ | D. | $\frac{1}{5}+\frac{2}{5}i$ |
6.设等差数列{an}的前n项和为Sn,若S9=54,则a2+a4+a9=( )
| A. | 9 | B. | 15 | C. | 18 | D. | 36 |